题目内容
在平面直角坐标系xOy中,动点P到直线l:x=2的距离是到点F(1,0)的距离的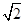 倍.
倍.
(1)求动点P的轨迹方程;
(2)设直线FP与(1)中曲线交于点Q,与l交于点A,分别过点P和Q作l的垂线,垂足为M,N,问:是否存在点P使得△APM的面积是△AQN面积的9倍?若存在,求出点P的坐标;若不存在,说明理由.
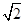 倍.
倍.(1)求动点P的轨迹方程;
(2)设直线FP与(1)中曲线交于点Q,与l交于点A,分别过点P和Q作l的垂线,垂足为M,N,问:是否存在点P使得△APM的面积是△AQN面积的9倍?若存在,求出点P的坐标;若不存在,说明理由.
(1)x2+2y2=2(2)存在点P为(0,±1)
(1)设点P的坐标为(x,y).
由题意知 =|2-x|,化简,得x2+2y2=2,所以动点P的轨迹方程为x2+2y2=2.
=|2-x|,化简,得x2+2y2=2,所以动点P的轨迹方程为x2+2y2=2.
(2)设直线FP的方程为x=ty+1,点P(x1,y1),Q(x2,y2),因为△AQN∽△APM,所以有PM=3QN,由已知得PF=3QF,所以有y1=-3y2,①
由 得(t2+2)y2+2ty-1=0,Δ=4t2+4(t2+2)=8>0
得(t2+2)y2+2ty-1=0,Δ=4t2+4(t2+2)=8>0
y1+y2=- ②,y1·y2=-
②,y1·y2=- ③,由①②③得t=-1,y1=1,y2=-
③,由①②③得t=-1,y1=1,y2=- 或t=1,y1=-1,y2=
或t=1,y1=-1,y2= ,所以存在点P为(0,±1).
,所以存在点P为(0,±1).
由题意知
 =|2-x|,化简,得x2+2y2=2,所以动点P的轨迹方程为x2+2y2=2.
=|2-x|,化简,得x2+2y2=2,所以动点P的轨迹方程为x2+2y2=2.(2)设直线FP的方程为x=ty+1,点P(x1,y1),Q(x2,y2),因为△AQN∽△APM,所以有PM=3QN,由已知得PF=3QF,所以有y1=-3y2,①
由
 得(t2+2)y2+2ty-1=0,Δ=4t2+4(t2+2)=8>0
得(t2+2)y2+2ty-1=0,Δ=4t2+4(t2+2)=8>0y1+y2=-
 ②,y1·y2=-
②,y1·y2=- ③,由①②③得t=-1,y1=1,y2=-
③,由①②③得t=-1,y1=1,y2=- 或t=1,y1=-1,y2=
或t=1,y1=-1,y2= ,所以存在点P为(0,±1).
,所以存在点P为(0,±1).
练习册系列答案
相关题目
 中,曲线
中,曲线 的参数方程为
的参数方程为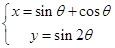 (
(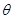 为参数),若以直角坐标系的原点
为参数),若以直角坐标系的原点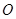 为极点,
为极点,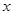 轴的正半轴为极轴建立极坐标,曲线
轴的正半轴为极轴建立极坐标,曲线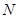 的极坐标方程为
的极坐标方程为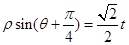 (其中
(其中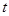 为常数).
为常数).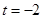 时,求曲线
时,求曲线 (
( 为参数)的倾斜角是
为参数)的倾斜角是 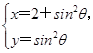 (θ为参数)化为普通方程.
(θ为参数)化为普通方程.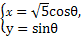 (0≤θ<π)和
(0≤θ<π)和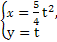 (t∈R),求它们的交点坐标.
(t∈R),求它们的交点坐标.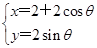 (θ为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l的方程为ρsin
(θ为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l的方程为ρsin 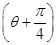 =2
=2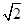 .
.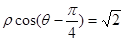 与圆
与圆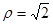 的公共点个数是________.
的公共点个数是________. 的方程为
的方程为 ,以极点为坐标原点,极轴为
,以极点为坐标原点,极轴为 轴的正半轴建立平面坐标系,圆
轴的正半轴建立平面坐标系,圆 的参数方程
的参数方程 (
( 为参数),若圆
为参数),若圆 .
. (
( 为参数)相交于
为参数)相交于 、
、 两点,则|
两点,则| |= .
|= .