题目内容
6名同学3名男生、3名女生分配到育才、育人、育红3所学校,育才学校只接收一名男生,另两所学校每所至少接收一名,则共有分配方案_________种.
90
根据乘法原理,先给育才选择一名男生共 ,然后给剩余的5名同学安排接受学校共
,然后给剩余的5名同学安排接受学校共 种,去除全部报育人和育红的情况,所以共有
种,去除全部报育人和育红的情况,所以共有 ×(
×( -2)=90种分配方案。
-2)=90种分配方案。
 ,然后给剩余的5名同学安排接受学校共
,然后给剩余的5名同学安排接受学校共 种,去除全部报育人和育红的情况,所以共有
种,去除全部报育人和育红的情况,所以共有 ×(
×( -2)=90种分配方案。
-2)=90种分配方案。
练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
 ,
, 必可表示成
必可表示成 的形式,其中
的形式,其中 .
. (sin
(sin +cos
+cos -
- )6展示式中含
)6展示式中含 项的系数是
项的系数是 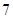 名男生中选取
名男生中选取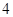 人参加
人参加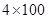 接力赛,要求甲、乙两人
接力赛,要求甲、乙两人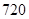
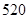
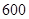
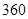
 方格,使得每行没有相同颜色且每列也没有相同颜色的涂法种数是 。
方格,使得每行没有相同颜色且每列也没有相同颜色的涂法种数是 。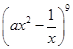 的展开式中常数项为84,其展开式中各项系数之和为__________.
的展开式中常数项为84,其展开式中各项系数之和为__________.