Question

已知O为坐标原点,  =(2asin²x,a), =(1,-2sinxcos x+1),F(x)= ·+b(a＜b且 a≠0),?

(1)求y=F(x)的单调递增区间;

(2)若F(x)的定义域为［,π］,值域为［２，５］，求a,b的值.

Answer 1

解:(1)f(x)= ·+b

=2asin²x-2asinxcosx+a+b??

=a(1-cos2x)-asin2x+a+b?

=-2asin(2x+)+2a+b.                                                                                      ?

a＞0时,由2kπ+≤2x+≤2kπ+(k∈Z),得y=f(x)的单调递增区间为［kπ+,kπ+ ］(k∈Z);                                                                                                       ?

a＜0时,由2kπ-≤2x+≤2kπ+ (k∈Z),得

y=f(x)的单调递增区间为［kπ-,kπ+］(k∈Z).?                                         ?

(2)f(x)=-2asin(2x+)+2a+b,?

x∈［,π］,2x+∈［,］,?

sin(2x+)∈［-1, ］.                                                                           ?

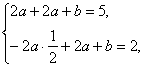a＞0时,得?

不满足a＜b,舍.                                                                                                      ?

a＜0时,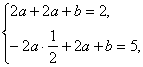得                                                            ?

综上,a=-1,b=6.