题目内容
【题目】已知函数
.
（1）求
的最小正周期；
（2）求在区间
上对称轴、对称中心及其最值.
【答案】(1)最小正周期为
(2)对称轴
，对称中心为
，最大值为
，最小值为
【解析】
(1)根据同角三角函数关系式的平方和关系、降幂公式、辅助角公式把函数的解析式化简成正弦型函数解析形式,最后根据最小正周期公式求出函数的最小正周期；
(2)利用正弦型函数的对称性和单调性,求出
在区间
上对称轴、对称中心及其最值
解：(1)因为
,
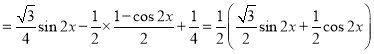
所以，函数的最小正周期为
.
(2)由(1)知
，
因为
，所以
，①
令
，得
，
所以，即为所求函数在上的对称轴；
令
，得
，所以
，
所以函数在上的对称中心为；（＊）
易判断函数在
上单调递增；在
上单调递增.
所以，
，
，
，
故函数在区间上最大值为，最小值为.
【另解】
接（＊）式
由①得
，所以
，
故函数在区间上最大值为，最小值为.
练习册系列答案
相关题目
