题目内容
已知函数 的定义域为
的定义域为 ,值域为[-1,2].
,值域为[-1,2].(1)求实数a,b的值;
(2)数列{an}中,有
 .则该数列有最大项、最小项吗?若有,求出数列的最大项、最小项;若没有,请说明理由.
.则该数列有最大项、最小项吗?若有,求出数列的最大项、最小项;若没有,请说明理由.
【答案】分析:(1)设 ,由
,由 ,知
,知 ,由
,由 ,知函数为
,知函数为 ,由此利用分类讨论思想能求出实数a,b的值.
,由此利用分类讨论思想能求出实数a,b的值.
(2)当 时,
时, ;当
;当 ,
, ,由此能求出数列的最大项、最小项.
,由此能求出数列的最大项、最小项.
解答:解:(1)设 ,
,
由 ,知
,知 ,…(2分)
,…(2分)
又 ,
,
则函数为 ,…(4分)
,…(4分)
即 ,…(5分)
,…(5分)
①当a>0时,g(t)在 单调递增,
单调递增,
有 ,得
,得 ; …(6分)
; …(6分)
②当a=0时,g(t)=b不合; …(7分)
③当a<0时,g(t)在 单调递减,
单调递减,
有 ,得
,得 ; …(8分)
; …(8分)
(2)①当 时,
时,
 ,
,
当n=7时,最小项为 ,
,
当n=8时,最大项为 ; …(11分)
; …(11分)
②当 时,
时,
 ,
,
当n=1时,最小项为 ,无最大项;…(14分)
,无最大项;…(14分)
点评:本题考查满足条件的实数值的求法,考查数列的最大项与最小项的求法,解题时要认真审题,注意数列和三角函数的综合应用,合理运用分类讨论思想、等价转化思想、数形结合思想进行解题.
 ,由
,由 ,知
,知 ,由
,由 ,知函数为
,知函数为 ,由此利用分类讨论思想能求出实数a,b的值.
,由此利用分类讨论思想能求出实数a,b的值.(2)当
 时,
时, ;当
;当 ,
, ,由此能求出数列的最大项、最小项.
,由此能求出数列的最大项、最小项.解答:解:(1)设
 ,
,由
 ,知
,知 ,…(2分)
,…(2分)又
 ,
,则函数为
 ,…(4分)
,…(4分)即
 ,…(5分)
,…(5分)①当a>0时,g(t)在
 单调递增,
单调递增,有
 ,得
,得 ; …(6分)
; …(6分)②当a=0时,g(t)=b不合; …(7分)
③当a<0时,g(t)在
 单调递减,
单调递减,有
 ,得
,得 ; …(8分)
; …(8分)(2)①当
 时,
时, ,
,当n=7时,最小项为
 ,
,当n=8时,最大项为
 ; …(11分)
; …(11分)②当
 时,
时, ,
,当n=1时,最小项为
 ,无最大项;…(14分)
,无最大项;…(14分)点评:本题考查满足条件的实数值的求法,考查数列的最大项与最小项的求法,解题时要认真审题,注意数列和三角函数的综合应用,合理运用分类讨论思想、等价转化思想、数形结合思想进行解题.

练习册系列答案
相关题目
已知函数 的定义域为
的定义域为 ,部分对应值如下表。
,部分对应值如下表。 的导函数
的导函数 的图像如图所示。
的图像如图所示。
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|

下列关于函数 的命题:
的命题:
①函数 在
在 上是减函数;②如果当
上是减函数;②如果当 时,
时, 最大值是
最大值是 ,那么
,那么 的最大值为
的最大值为 ;③函数
;③函数 有
有 个零点,则
个零点,则 ;④已知
;④已知 是
是 的一个单调递减区间,则
的一个单调递减区间,则 的最大值为
的最大值为 。
。
其中真命题的个数是( )
A、4个 B、3个 C、2个 D、1个
 的定义域为
的定义域为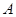 ,
,  ,且
,且 的真子集,求实数
的真子集,求实数 的取值范围.
的取值范围.




 的定义域为
的定义域为 ,且
,且 ,
, 为
为 ,
, 满足
满足 ,则
,则 的取值范围是
的取值范围是
 B.
B. C.
C. D.
D.