题目内容
有一个公用电话亭,在观察使用这个电话的人的流量时,设在某一时刻,有n个人正在使用电话或等待使用的概率为P(n),且P(n)与时刻t无关,统计得到P(n)= ,那么在某一时刻,这个公用电话亭时一个人也没有的概率P(0)的值是________.
,那么在某一时刻,这个公用电话亭时一个人也没有的概率P(0)的值是________.

分析:由题意,公用电话亭每次不超过5人正在使用电话或等待使用,有0、1、2、3、4或5个人正在使用电话或等待使用是必然事件,且各种情种的概率和是1,又由题目所给的分段函数式得到P(1)=
 P(0),P(2)=
P(0),P(2)= P(0),P(3)=
P(0),P(3)= P(0),P(4)=
P(0),P(4)= P(0),P(5)=
P(0),P(5)= P(0),算出答案.
P(0),算出答案.解答:由题意知:本公用电话亭每次不超过3人正在使用电话或等待使用,
∴“有0、1、2、3、4或5个正在使用电话或等待使用“是必然事件,
∴P(0)+P(1)+P(2)+P(3)+P(4)+P(5)=1,
∵P(1)=
 P(0),P(2)=
P(0),P(2)= P(0),P(3)=
P(0),P(3)= P(0),P(4)=
P(0),P(4)= P(0),P(5)=
P(0),P(5)= P(0),
P(0),∴P(0)+
 P(0)+
P(0)+ P(0)+
P(0)+ P(0)+
P(0)+ P(0)+
P(0)+ P(0)=1,
P(0)=1,即
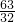 P(0)=1,
P(0)=1,∴P(0)=
 ,
,故答案为:
 .
.点评:本题考查的是等可能事件概率,属于中档题.题中所给的分段函数这个条件容易使人出错,要求运用从具体到抽象、从特殊到一般的辩证唯物主义观点分析问题的能力,充分体现数学的化归思想.

练习册系列答案
相关题目
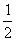 那么在某一时刻,这个公用电话亭里一个人也没有的概率P(0)的值是_______________.
那么在某一时刻,这个公用电话亭里一个人也没有的概率P(0)的值是_______________.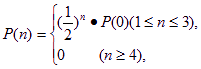 那么在某一时刻,这个公用电话亭里一个人也没有的概率是___________.
那么在某一时刻,这个公用电话亭里一个人也没有的概率是___________.