题目内容
集合P= ,则P∩Q=
,则P∩Q=
- A.[0,+∞)
- B.
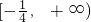
- C.[2,+∞)
- D.φ
A
分析:由题可知集合P与Q中的元素都为函数的值域,分别求出两个函数的值域,并求出公共解集即可得到P∩Q.
解答:由题可知:集合P中的元素为x=a2-3a+2,a∈R时的值域,
因为此函数为开口向上的抛物线,函数有最小值为x=- ,
,
所以集合P={x|x≥- };
};
而集合Q中的元素为y= 的值域为[0,+∞),
的值域为[0,+∞),
所以P∩Q=[0,+∞),
故选A.
点评:让学生理解代表元的意义,这是个易错点,需要强化.掌握函数值域的求法,理解交集的定义及会进行交集的运算.
分析:由题可知集合P与Q中的元素都为函数的值域,分别求出两个函数的值域,并求出公共解集即可得到P∩Q.
解答:由题可知:集合P中的元素为x=a2-3a+2,a∈R时的值域,
因为此函数为开口向上的抛物线,函数有最小值为x=-
 ,
,所以集合P={x|x≥-
 };
};而集合Q中的元素为y=
 的值域为[0,+∞),
的值域为[0,+∞),所以P∩Q=[0,+∞),
故选A.
点评:让学生理解代表元的意义,这是个易错点,需要强化.掌握函数值域的求法,理解交集的定义及会进行交集的运算.

练习册系列答案
相关题目
集合P={x|y=
},集合Q={y|y=
},则P与Q的关系是( )
| x+1 |
| x-1 |
| A、P=Q | B、P?Q |
| C、P⊆Q | D、P∩Q=∅ |
 ,则P∩Q=( )
,则P∩Q=( )