题目内容
在周长为定值的![]() 中,已知
中,已知![]() ,且当顶点
,且当顶点![]() 位于定点
位于定点![]() 时,
时,![]() 有最小值为
有最小值为![]() .(1)建立适当的坐标系,求顶点
.(1)建立适当的坐标系,求顶点![]() 的轨迹方程.(2)过点
的轨迹方程.(2)过点![]() 作直线与(1)中的曲线交于
作直线与(1)中的曲线交于![]() 、
、![]() 两点,求
两点,求![]() 的最小值的集合.
的最小值的集合.
![]() 的最小值的集合为空集.
的最小值的集合为空集.
解析:
(1) 以AB所在直线为x轴,线段AB的中垂线为y轴建立直角坐标系,设 |CA|+|CB|=2a(a>3)为定值,所以C点的轨迹是以A、B为焦点的椭圆,所以焦距 2c=|AB|=6.
因为 ![]()
又 ![]() ,所以
,所以 ![]() ,由题意得
,由题意得 ![]() .
.
此时,|PA|=|PB|,P点坐标为 P(0,±4).所以C点的轨迹方程为 ![]()
(2) 不妨设A点坐标为A(-3,0),M(x1,y1),N(x2,y2).当直线MN的倾斜角不为900时,设其方程为 y=k(x+3) 代入椭圆方程化简,得 ![]()
显然有 △≥0, 所以 ![]()
而由椭圆第二定义可得 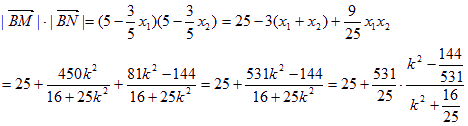
只要考虑 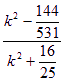 的最小值,即考虑
的最小值,即考虑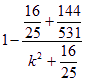 取最小值,显然.
取最小值,显然.
当k=0时,![]() 取最小值16.
取最小值16.
当直线MN的倾斜角为900时,x1=x2=-3,得 ![]()
但 ![]() ,故
,故![]() ,这样的M、N不存在,即
,这样的M、N不存在,即![]() 的最小值的集合为空集.
的最小值的集合为空集.

练习册系列答案
相关题目
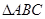 中,已知
中,已知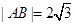 ,动点
,动点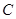 的运动轨迹为曲线G,且当动点
的运动轨迹为曲线G,且当动点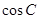 有最小值
有最小值 .
.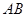 所在直线为
所在直线为 轴,线段
轴,线段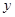 轴建立直角坐标系,求曲线G的方程.
轴建立直角坐标系,求曲线G的方程. 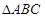 中,已知
中,已知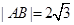 ,动点
,动点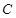 的运动轨迹为曲线G,且当动点
的运动轨迹为曲线G,且当动点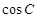 有最小值
有最小值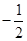 .
.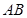 所在直线为
所在直线为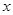 轴,线段
轴,线段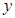 轴建立直角坐标系,求曲线
轴建立直角坐标系,求曲线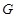 的方程;
的方程;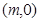 作圆
作圆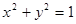 的切线
的切线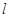 交曲线
交曲线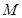 ,
,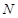 两点.将线段MN的长|MN|表示为
两点.将线段MN的长|MN|表示为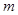 的函数,并求|MN|的最大值.
的函数,并求|MN|的最大值.