题目内容
已知x、y之间满足
+
=1(b>0)
(1)方程
+
=1(b>0)表示的曲线经过一点(
,
),求b的值
(2)动点(x,y)在曲线
+
=1(b>0)上变化,求x2+2y的最大值;
(3)由
+
=1(b>0)能否确定一个函数关系式y=f(x),如能,求解析式;如不能,再加什么条件就可使x、y之间建立函数关系,并求出解析式.
| x2 |
| 4 |
| y2 |
| b2 |
(1)方程
| x2 |
| 4 |
| y2 |
| b2 |
| 3 |
| 1 |
| 2 |
(2)动点(x,y)在曲线
| x2 |
| 4 |
| y2 |
| b2 |
(3)由
| x2 |
| 4 |
| y2 |
| b2 |
(1)由题意可得:曲线经过一点(
,
),
所以
+
=1(b>0),
解得:b=1.(4分)
(2)根据
+
=1(b>0)得x2=4(1-
)(5分)
所以x2+2y=4(1-
)+2y=-
(y-
)2+
+4(-b≤y≤b)(7分)
当
≥b时,即b≥4时(x2+2y)max=2b+4,
当
≤b时,即0≤b≤4时(x2+2y)max=
+4
∴(x2+2y)max=
(10分)
(2)不能; (11分)
如再加条件xy<0就可使x、y之间建立函数关系,(12分)
并且解析式y=
.(14分)
| 3 |
| 1 |
| 2 |
所以
| ||
| 4 |
| 1 |
| 4b2 |
解得:b=1.(4分)
(2)根据
| x2 |
| 4 |
| y2 |
| b2 |
| y2 |
| b2 |
所以x2+2y=4(1-
| y2 |
| b2 |
| 4 |
| b2 |
| b2 |
| 4 |
| b2 |
| 4 |
当
| b2 |
| 4 |
当
| b2 |
| 4 |
| b2 |
| 4 |
∴(x2+2y)max=
|
(2)不能; (11分)
如再加条件xy<0就可使x、y之间建立函数关系,(12分)
并且解析式y=
|

练习册系列答案
相关题目
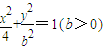
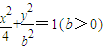 表示的曲线经过一点
表示的曲线经过一点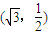 ,求b的值
,求b的值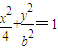 (b>0)上变化,求x2+2y的最大值;
(b>0)上变化,求x2+2y的最大值;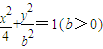 能否确定一个函数关系式y=f(x),如能,求解析式;如不能,再加什么条件就可使x、y之间建立函数关系,并求出解析式.
能否确定一个函数关系式y=f(x),如能,求解析式;如不能,再加什么条件就可使x、y之间建立函数关系,并求出解析式.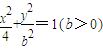
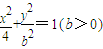 表示的曲线经过一点
表示的曲线经过一点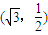 ,求b的值
,求b的值 (b>0)上变化,求x2+2y的最大值.
(b>0)上变化,求x2+2y的最大值.