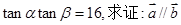题目内容
已知函数f(x)=(1+ )sin2x+
)sin2x+ sin(x+
sin(x+ )sin(x-
)sin(x- ).
).
(1)当 =0时,求f(x)在区间[
=0时,求f(x)在区间[ ,
, ]上的取值范围;
]上的取值范围;
(2)当tan =2时,f(
=2时,f( )=
)= ,求
,求 的值.
的值.
 )sin2x+
)sin2x+ sin(x+
sin(x+ )sin(x-
)sin(x- ).
).(1)当
 =0时,求f(x)在区间[
=0时,求f(x)在区间[ ,
, ]上的取值范围;
]上的取值范围;(2)当tan
 =2时,f(
=2时,f( )=
)= ,求
,求 的值.
的值.(1)[0, ];(2)-2.
];(2)-2.
 ];(2)-2.
];(2)-2.本试题主要考查了三角函数的性质和三角方程的求解的综合运用。
解: (1)当m=0时,f(x)=sin2x+sinxcosx= (sin2x-cos2x)+
(sin2x-cos2x)+
= sin(2x-
sin(2x- )+
)+ ,……………………(3分)
,……………………(3分)
又由x∈[ ,
, ]得2x-
]得2x- ∈[0,
∈[0, ],所以sin(2x-
],所以sin(2x- )∈[-
)∈[- ,1],
,1],
从而f(x)= sin(2x-
sin(2x- )+
)+ ∈[0,
∈[0, ].……………………(6分)
].……………………(6分)
(2)f(x)=sin2x+sinxcosx- cos2x=
cos2x=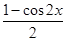 +
+ sin2x-
sin2x- cos2x
cos2x
= [sin2x-(1+m)cos2x]+
[sin2x-(1+m)cos2x]+ ,………………………………(8分)
,………………………………(8分)
由tanα=2得sin2α= =
= =
= ,
,
cos2α= =
= =-
=- ,……………………(10分)
,……………………(10分)
所以f(α)= =
= [
[ +(1+m)
+(1+m) ]+
]+ ,得m=-2.………………(12分)
,得m=-2.………………(12分)
解: (1)当m=0时,f(x)=sin2x+sinxcosx=
 (sin2x-cos2x)+
(sin2x-cos2x)+
=
 sin(2x-
sin(2x- )+
)+ ,……………………(3分)
,……………………(3分)又由x∈[
 ,
, ]得2x-
]得2x- ∈[0,
∈[0, ],所以sin(2x-
],所以sin(2x- )∈[-
)∈[- ,1],
,1],从而f(x)=
 sin(2x-
sin(2x- )+
)+ ∈[0,
∈[0, ].……………………(6分)
].……………………(6分)(2)f(x)=sin2x+sinxcosx-
 cos2x=
cos2x=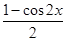 +
+ sin2x-
sin2x- cos2x
cos2x=
 [sin2x-(1+m)cos2x]+
[sin2x-(1+m)cos2x]+ ,………………………………(8分)
,………………………………(8分)由tanα=2得sin2α=
 =
= =
= ,
,cos2α=
 =
= =-
=- ,……………………(10分)
,……………………(10分)所以f(α)=
 =
= [
[ +(1+m)
+(1+m) ]+
]+ ,得m=-2.………………(12分)
,得m=-2.………………(12分)
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
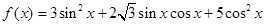 .
.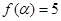 ,求
,求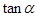 的值;
的值;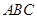 三内角
三内角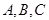 所对边分别为
所对边分别为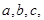 且
且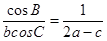 ,求
,求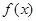 在
在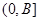 上的值域.
上的值域. ,则
,则 =( )
=( )





 ,求
,求 的值
的值 ,求
,求 的值
的值 中,三个内角
中,三个内角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,其中
,其中 , 且
, 且
 过
过 三点,点
三点,点 位于劣弧上,求
位于劣弧上,求 面积最大值.
面积最大值.
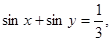 则
则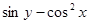 的是________.
的是________. =( )
=( ) 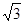 cosα
cosα 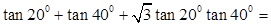 ( )
( )

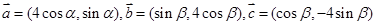
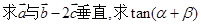 的值;
的值;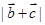 的最大值;(3)若
的最大值;(3)若