题目内容
设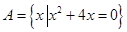
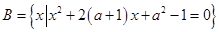 .
.
(1)若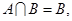 求a的值;
求a的值;
(2)若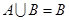 ,求a的值;
,求a的值;
【答案】
(1) 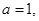 或
或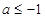 ;(2)
;(2) 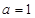
【解析】
试题分析:(1)由解出集合A.又因为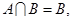 可得
可得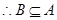 .所以分两类为空集. 其一集合B.则只需二次方程的判别式小于零即可;其二集合B不是空集.则至少存在集合A中的一个元素-4,或0通过列举分类以及带入验证即可求得
.所以分两类为空集. 其一集合B.则只需二次方程的判别式小于零即可;其二集合B不是空集.则至少存在集合A中的一个元素-4,或0通过列举分类以及带入验证即可求得 的值.
的值.
(2)因为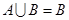
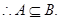 由于一个二次方程至多两个实数根,所以集合A与集合B相等.所以两个方程要相同,所以可得
由于一个二次方程至多两个实数根,所以集合A与集合B相等.所以两个方程要相同,所以可得 .
.
试题解析:由已知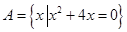 得
得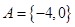
(1) 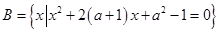 .
.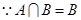 ,
,
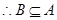 . ①若
. ①若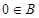 ,则
,则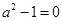 ,
,
解得 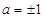 . 当
. 当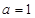 时,B=A ;
时,B=A ;
当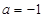 时,
时, 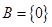 ②
②
若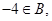 则
则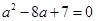 ,
,
解得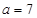 或
或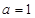 ,当
,当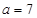 时,
时, 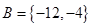 ,
,
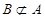 .
③
.
③
若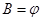 ,则△
,则△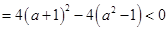 ,解得;
,解得; 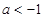 ,
,
由①②③得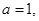 或
或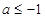 ,
,
(2) 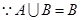
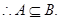
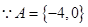 B至多有两个元素,
B至多有两个元素, 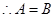 ,由(1)知,
,由(1)知, 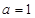
考点:1.集合的运算交集,并集.2.二次方程的求解.3.分类讨论问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的不等式
的不等式 的解集为A .
的解集为A . , 求A ;
, 求A ; ,
求实数
,
求实数 的取值范围;
的取值范围; ”是“
”是“ ”的必要不充分条件, 求实数
”的必要不充分条件, 求实数