题目内容
14.已知点P为直线l:x-2y-3=0 上的动点,A(0,1),B(4,3),则|AP|+|BP|的最小值为( )| A. | 2$\sqrt{5}$ | B. | 5$\sqrt{2}$ | C. | 6 | D. | 2$\sqrt{10}$ |
分析 由题意画出图形,把|AP|+|BP|的最小值转化为B到A关于直线l的对称点的距离得答案.
解答 解:如图,
设A(0,1)关于直线l:x-2y-3=0的对称点为C(m,n),
则$\left\{\begin{array}{l}{\frac{m}{2}-2×\frac{n+1}{2}-3=0}\\{\frac{n-1}{m}=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=2}\\{n=-3}\end{array}\right.$,
∴C(2,-3),又B(4,3),
则|AP|+|BP|的最小值为|BC|=$\sqrt{(2-4)^{2}+(-3-3)^{2}}=2\sqrt{10}$.
故选:D.
点评 本题考查直线上动点到两定点连线距离最小值问题,考查了数学转化思想方法,训练了两点间距离公式的应用,是基础题.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
2.函数f(x)=x3-3x在[-3,$\frac{3}{2}$]上的最大值和最小值分别是( )
| A. | 2,-2 | B. | 2,-18 | C. | 18,-2 | D. | 18,-18 |
3.下列判断错误的是( )
| A. | 命题“p且q”的否定命题是“¬p或¬q” | |
| B. | 已知a∈R且a≠0,则“$\frac{1}{a}$<1”是“a>1”的充要条件 | |
| C. | 集合A={a,b,c},集合B={0,1},则从集合A到集合B的不同映射个数为8个 | |
| D. | 命题p:若M∪N=M,则N?M,命题q:5∉{2,3},则命题“p且q”为假 |
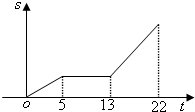 某同学来学校上学,时间t(分钟)与路程s(米)的函数关系如图所示,现有如下几种说法:
某同学来学校上学,时间t(分钟)与路程s(米)的函数关系如图所示,现有如下几种说法: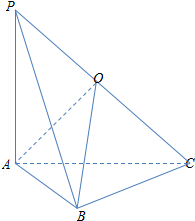 如图,已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,且AB=BC=1,PA=$\sqrt{2}$,O为线段PC的中点,
如图,已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,且AB=BC=1,PA=$\sqrt{2}$,O为线段PC的中点,