题目内容
4.已知M,N为y轴正半轴上的两个动点,点P(异于原点O)为x轴上的一个定点,若以MN为直径的圆与圆(x-3)2+y2=4相外切,且∠MPN的大小恒为定值,则线段OP的长为$\sqrt{5}$.分析 设以MN为直径的圆的圆心为O2(0,a),半径为r,OP=t,由两圆外切和∠MPN的大小恒为定值可得.
解答 解:设以MN为直径的圆的圆心为O2(0,a),半径为r,OP=t,
则tan∠OPM=$\frac{a-r}{t}$,tan∠OPN=$\frac{a+r}{t}$,
∴tan∠MPN=tan(∠OPN-∠OPM)
=$\frac{\frac{a+r}{t}-\frac{a-r}{t}}{1+\frac{a+r}{t}•\frac{a-r}{t}}$=$\frac{2rt}{{t}^{2}+{a}^{2}-{r}^{2}}$,
∵两圆外切,∴$\sqrt{{a}^{2}+9}$=|r+2|,
∴a2=(r+2)2-9,
∴tan∠MPN=$\frac{2rt}{{t}^{2}+{a}^{2}-{r}^{2}}$=$\frac{2t}{\frac{{t}^{2}-5}{r}+4}$,
∵∠MPN的大小恒为定值,∴t=$\sqrt{5}$
故答案为:$\sqrt{5}$
点评 本题考查圆与圆的位置关系,涉及两角差的正切公式,属中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
15.函数f(x)=ax2+bx+c的图象如图所示,M=|a-b+c|+|2a+b|,N=|a+b+c|+|2a-b|则( )


| A. | M>N? | B. | M=N? | ||
| C. | M<N? | D. | M、N 的大小关系不确定 |
9.若函数f(x)是定义在R上的偶函数,在(-∞,0]上是减函数,且f(2)=0,则使得(x-2)f(x)<0的x的取值范围是( )
| A. | (-∞,-2) | B. | (2,+∞) | C. | (-∞,-2)∪(2,+∞) | D. | (-2,2) |
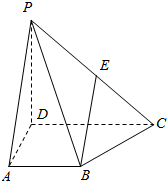 四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,AD⊥DC,侧棱PD⊥底面ABCD,且AB=AD=1,PD=DC=2,E是PC的中点.
四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,AD⊥DC,侧棱PD⊥底面ABCD,且AB=AD=1,PD=DC=2,E是PC的中点.