题目内容
已知向量 =(cosωx,-cosωx),
=(cosωx,-cosωx), =(
=( sinωx,cosωx),其中ω<0为常数。设函数f(x)=
sinωx,cosωx),其中ω<0为常数。设函数f(x)= +
+ (x∈R),若函数f(x)的最小正周期为π。
(x∈R),若函数f(x)的最小正周期为π。
(1)求ω的值;
(2)若当x∈[0, ]时,不等式|k+f(x)|<4恒成立,求实数k的取值范围。
]时,不等式|k+f(x)|<4恒成立,求实数k的取值范围。
 =(cosωx,-cosωx),
=(cosωx,-cosωx), =(
=( sinωx,cosωx),其中ω<0为常数。设函数f(x)=
sinωx,cosωx),其中ω<0为常数。设函数f(x)= +
+ (x∈R),若函数f(x)的最小正周期为π。
(x∈R),若函数f(x)的最小正周期为π。 (1)求ω的值;
(2)若当x∈[0,
 ]时,不等式|k+f(x)|<4恒成立,求实数k的取值范围。
]时,不等式|k+f(x)|<4恒成立,求实数k的取值范围。 解:(1)由题设,
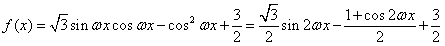
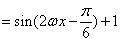 ,
,
因为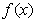 的最小正周期为
的最小正周期为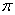 ,
,
所以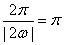 ,即
,即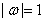 ,
,
又ω<0,所以ω=-1。
(2) 由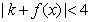 得,
得,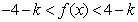 恒成立,
恒成立,
据题意,当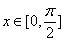 时,
时,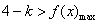 ,且
,且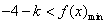 ,
,
因为ω=-1,所以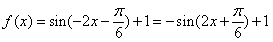 ,
,
当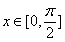 时,
时,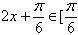 ,
,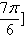 ,即
,即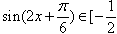 ,
,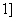 ,
,
所以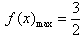 ,
,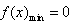 ,
,
从而有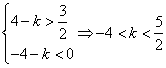 ,
,
故k的取值范围是(-4,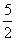 )。
)。
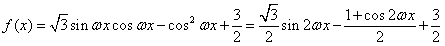
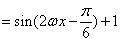 ,
,因为
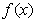 的最小正周期为
的最小正周期为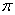 ,
,所以
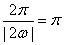 ,即
,即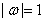 ,
,又ω<0,所以ω=-1。
(2) 由
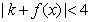 得,
得,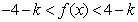 恒成立,
恒成立,据题意,当
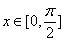 时,
时,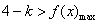 ,且
,且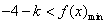 ,
,因为ω=-1,所以
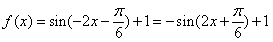 ,
,当
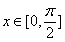 时,
时,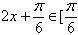 ,
,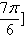 ,即
,即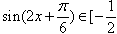 ,
,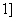 ,
,所以
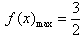 ,
,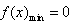 ,
,从而有
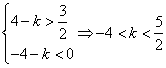 ,
,故k的取值范围是(-4,
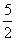 )。
)。 
练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
已知向量
=(cosα,sinα),
=(cosβ,sinβ),若|
-
|=
,则
和
的夹角为( )
| a |
| b |
| a |
| b |
| 2 |
| a |
| b |
| A、60° | B、90° |
| C、120° | D、150° |