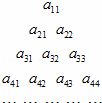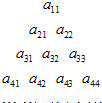题目内容
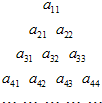 将如图所示的三角形数阵中所有的数按从上至下、从左至右的顺序排列成数列a11,a21,a22,a31,a32,….若所得数列构成一个等差数列,且a11=2,a33=12,则
将如图所示的三角形数阵中所有的数按从上至下、从左至右的顺序排列成数列a11,a21,a22,a31,a32,….若所得数列构成一个等差数列,且a11=2,a33=12,则①数阵中的数aii可用i表示为
i2+i
i2+i
;②若amn+a(m+1)(n+1)=a(m+2)(n+2),则m+n的值为
5
5
.分析:①不妨设等差数列a11,a21,a22,a31,a32,…为{bn},则由a11=2,a33=12可得b1=2,公差d=2,故bn=2n.而 aii可为等差数列{bn}中的第1+2+3+…+i=
个,由此可得 aii 的值.
②先求出amn=m2-m+2n.再由已知的等式化简可得 m2-3m-4+2n=0,由于n>0,可得m2-3m-4<0,解得m的范围,结合 m≥n>0,可得m和n的值,从而求得 m+n的值.
| i(i+1) |
| 2 |
②先求出amn=m2-m+2n.再由已知的等式化简可得 m2-3m-4+2n=0,由于n>0,可得m2-3m-4<0,解得m的范围,结合 m≥n>0,可得m和n的值,从而求得 m+n的值.
解答:解:①不妨设等差数列a11,a21,a22,a31,a32,…为{bn},则由a11=2,a33=12可得b1=2,公差d=2.
故bn=2n.
而 aii可为等差数列{bn}中的第1+2+3+…+i=
个,∴aii =2×
=i(i+1)=i2+i,
故答案为 i2+i.
②由题意可得,amn=b1+2+3+…+(m-1)+n=2[1+2+3+…+(m-1)+n]=m2-m+2n.
∴a(m+1)(n+1)=(m+1)2-(m+1)+2(n+1),a(m+2)(n+2)=(m+2)2-(m+2)+2(n+2).
再由 amn+a(m+1)(n+1)=a(m+2)(n+2),
可得 m2-m+2n+(m+1)2-(m+1)+2(n+1)=(m+2)2-(m+2)+2(n+2),
化简可得 m2-3m-4+2n=0,由于n>0,∴m2-3m-4<0,解得-1<m<4,
∴m=1,2,3,再由 m≥n>0,可得
,∴m+n=5,
故答案为 5.
故bn=2n.
而 aii可为等差数列{bn}中的第1+2+3+…+i=
| i(i+1) |
| 2 |
| i(i+1) |
| 2 |
故答案为 i2+i.
②由题意可得,amn=b1+2+3+…+(m-1)+n=2[1+2+3+…+(m-1)+n]=m2-m+2n.
∴a(m+1)(n+1)=(m+1)2-(m+1)+2(n+1),a(m+2)(n+2)=(m+2)2-(m+2)+2(n+2).
再由 amn+a(m+1)(n+1)=a(m+2)(n+2),
可得 m2-m+2n+(m+1)2-(m+1)+2(n+1)=(m+2)2-(m+2)+2(n+2),
化简可得 m2-3m-4+2n=0,由于n>0,∴m2-3m-4<0,解得-1<m<4,
∴m=1,2,3,再由 m≥n>0,可得
|
故答案为 5.
点评:本题主要考查等差数列的性质,等差数列的前n项和公式的应用,一元二次不等式的解法,属于中档题.

练习册系列答案
 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
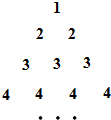 将如图所示的三角形数阵中的数按从小到大的顺序排列:1,2,2,3,3,3,4,4,4,4,…,记为数列{an},记数列{an}前2k2(k∈N+)项的和为bk,可以推测:
将如图所示的三角形数阵中的数按从小到大的顺序排列:1,2,2,3,3,3,4,4,4,4,…,记为数列{an},记数列{an}前2k2(k∈N+)项的和为bk,可以推测: 将正整数按一定的规则排成了如图所示的三角形数阵.根据这个排列规则,数阵中第20行从左至右的第3个数是( )
将正整数按一定的规则排成了如图所示的三角形数阵.根据这个排列规则,数阵中第20行从左至右的第3个数是( )