题目内容
(2011•东城区一模)设f(x)=
且f(2
)=1,则a=
|
| 2 |
7
7
;f(f(2))=6
6
.分析:由f(x)=
,知f(2
)=loga[(2
)2-1]=loga7,再由f(2
)=1,知loga7=1,所以a=7;故f(f(2))=f(log73)=2×7log73,由此能求出f(f(2)).
|
| 2 |
| 2 |
| 2 |
解答:解:∵f(x)=
,
∴f(2
)=loga[(2
)2-1]
=loga7,
∵f(2
)=1,
∴loga7=1,
∴a=7;
∴f(f(2))=f[log7(4-1)]
=f(log73)
=2×7log73
=2×3=6.
故答案为:7,6.
|
∴f(2
| 2 |
| 2 |
=loga7,
∵f(2
| 2 |
∴loga7=1,
∴a=7;
∴f(f(2))=f[log7(4-1)]
=f(log73)
=2×7log73
=2×3=6.
故答案为:7,6.
点评:本题考查对数的运算性质,是基础题.解题时要认真审题,仔细解答,注意分段函数的性质和应用.

练习册系列答案
相关题目
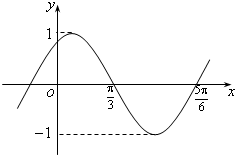 (2011•东城区一模)已知函数y=sin(ωx+φ)
(2011•东城区一模)已知函数y=sin(ωx+φ)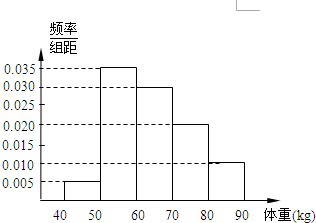 (2011•东城区一模)从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图).由图中数据可知体重的平均值为
(2011•东城区一模)从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图).由图中数据可知体重的平均值为