题目内容

（2011•东城区一模）过抛物线y2=2px（p＞0）的焦点作倾斜角为60°的直线，与抛物线分别交于A，B两点（点A在x轴上方），
|AF||BF|
=
3
3
．
分析：设出A、B坐标，利用抛物线焦半径公式求出|AB|，结合抛物线的性质x1x2=
p2
4
，求出A、B的坐标，然后求比值
|AF|
|BF|
即可．
解答：解：设A（x1，y1），B（x2，y2），则
|AB|=x1+x2+p=
2p
sin2θ
=
8p
3
，x1+x2=
5p
3
，
又 x1x2=
p2
4
，可得 x1=
3
2
p，x2=
p
6
，
则
|AF|
|BF|
=
3p
2
+
p
2
p
2
+
p
6
=3，
故答案为：3．
点评：本题主要考察了直线与抛物线的位置关系，抛物线的简单性质，特别是焦点弦问题，解题时要善于运用抛物线的定义解决问题．
练习册系列答案
相关题目
（2011•东城区一模）已知α∈(
π
2
，π)，tan(α+
π
4
)=
1
7
，那么sinα+cosα的值为（　　）
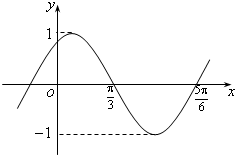（2011•东城区一模）已知函数y=sin（ωx+φ）(ω＞0， 0＜φ≤
π
2
)的部分图象如图所示，则点P（ω，φ）的坐标为（　　）
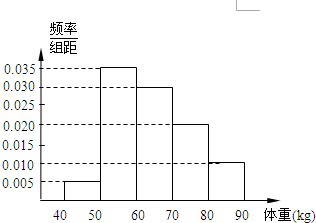（2011•东城区一模）从某地高中男生中随机抽取100名同学，将他们的体重（单位：kg）数据绘制成频率分布直方图（如图）．由图中数据可知体重的平均值为
64.5
64.5
kg；若要从体重在[60，70），[70，80），[80，90]三组内的男生中，用分层抽样的方法选取12人参加一项活动，再从这12人选两人当正、负队长，则这两人身高不在同一组内的概率为
2
3
2
3
．
（2011•东城区一模）对于n∈N*（n≥2），定义一个如下数阵：Ann=
a11a12…a1n
a21a22…a2n
…………
an1an2…ann

其中对任意的1≤i≤n，1≤j≤n，当i能整除j时，aij=1；当i不能整除j时，aij=0．
（Ⅰ）当n=4时，试写出数阵A44；
（Ⅱ）设t(j)=
n
i=1
aij=a1j+a2j+…+anj．若[x]表示不超过x的最大整数，
求证：
n
j=1
t(j)=
n
i=1
[ 
n
i
 ]．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网