题目内容
已知函数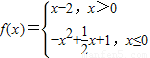 ,则函数g(x)=f(x)+x的零点的个数是 个.
,则函数g(x)=f(x)+x的零点的个数是 个.
【答案】分析:函数g(x)=f(x)+x的零点,即方程f(x)=-x的根.因此分x>0和x≤0两种情况,结合分段函数的表达式建立关于x的方程,解之即可得到方程的根,从而得到函数g(x)=f(x)+x的零点的情况,得到本题答案.
解答:解:函数g(x)=f(x)+x的零点,即方程f(x)=-x的根
①当x>0时,由x-2=-x,解得x=1;
②当x≤0时,由-x2+ x+1=-x,解得x=-
x+1=-x,解得x=- (舍去x=2)
(舍去x=2)
综上所述,方程f(x)=-x的根为x=- 或x=1,共两个
或x=1,共两个
由此可得数g(x)=f(x)+x的零点的个数是2个
故答案为:2
点评:本题给出分段函数,讨论与其有关的方程根的个数,着重考查了函数零点的含义和方程的解法等知识,属于基础题.
解答:解:函数g(x)=f(x)+x的零点,即方程f(x)=-x的根
①当x>0时,由x-2=-x,解得x=1;
②当x≤0时,由-x2+
 x+1=-x,解得x=-
x+1=-x,解得x=- (舍去x=2)
(舍去x=2)综上所述,方程f(x)=-x的根为x=-
 或x=1,共两个
或x=1,共两个由此可得数g(x)=f(x)+x的零点的个数是2个
故答案为:2
点评:本题给出分段函数,讨论与其有关的方程根的个数,着重考查了函数零点的含义和方程的解法等知识,属于基础题.

练习册系列答案
相关题目
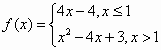 ,则函数g(x)=f(x)-log4x的零点个数为________.
,则函数g(x)=f(x)-log4x的零点个数为________.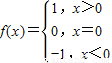 ,则函数g(x)=x2f(x-1)的值域是( )
,则函数g(x)=x2f(x-1)的值域是( )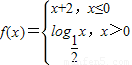 ,则函数g(x)=f(x)-x的零点有( )
,则函数g(x)=f(x)-x的零点有( ) ,则函数g(x)=f(x)-2的零点是 .
,则函数g(x)=f(x)-2的零点是 .