题目内容
15.先后抛掷两枚均匀的正方体骰子,观察向上的点数,问:(1)共有多少种不同的结果?
(2)所得点数之和是11的概率是多少?
(3)所得点数之和是4的倍数的概率是多少?
分析 (1)一共有6×6=36(种)不同的结果,
(2)所得点数之和为11记为事件A,有(5,6),(6,5)两种,根据公式计算即可,
(3)所得点数之和是4的倍数为事件B,则事件B的结果有9种,根据公式计算即可.
解答 解:(1)一共有6×6=36(种)不同的结果.
(2)所得点数之和为11记为事件A,有(5,6),(6,5),故P(A)=$\frac{2}{36}$=$\frac{1}{18}$,
(3)所得点数之和是4的倍数为事件B,则事件B的结果有12种,故所求的概率为P(B)=$\frac{9}{36}$=$\frac{1}{4}$.
点评 本题考查了古典概型概率问题,关键是列举,属于基础题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
3.己知函数f(x)=x3+ax+$\frac{1}{4}$,g(x)=-lnx用min{m,n}表示m,n中的最小值,设函数h(x)=min﹛(f(x),g(x)} (x>0),则当-$\frac{5}{4}$<a<-$\frac{3}{4}$时,h(x)的零点个数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
10.执行如图所示的程序框图,则输出的结果是( )
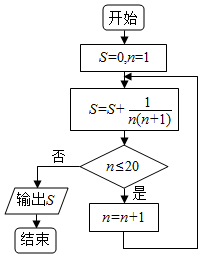

| A. | $\frac{22}{23}$ | B. | $\frac{21}{22}$ | C. | $\frac{20}{21}$ | D. | $\frac{19}{20}$ |