Question

【题目】如图，在半径为 ，圆心角为60°的扇形的弧上任取一点P，作扇形的内接矩形PNMQ，使点Q在OA上，点N，M在OB上，设矩形PNMQ的面积为y，∠POB=θ．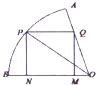

（1）将y表示成θ的函数关系式，并写出定义域；
（2）求矩形PNMQ的面积取得最大值时 的值；
（3）求矩形PNMQ的面积y≥ 的概率．

Answer 1

【答案】
（1）解：在Rt△PON中，∠PNO=90°，∠POB=θ， ，

所以 ， ，

在Rt△QMO中，∠QMO=90°，∠QON=60°，QM=PN=

所以OM=

所以：MN=ON﹣OM=

所以y=

即：y=3sinθcosθ﹣ sin2θ，（ ）

（2）解：由（1）得y=3sinθcosθ﹣ sin2θ= ﹣

= ）﹣ =

∵θ∈（0， ）

∴

∴sin（ ）∈

∴ ，即 时，y的最大值为 ．

此时ON= cos = = ，则 =| || |cos = × = ．

（3）解：若矩形PNMQ的面积y≥ ，

则 ≥ ，

即 sin（ ）≥ ，

则sin（ ）≥ ，

∵

∴ ≤ ≤ ，

即 ≤θ≤ ，

则对应的概率P= =

【解析】（1）利用三角函数的关系，求出矩形的邻边，求出面积的表达式，化为一个角的一个三角函数的形式，根据θ的范围确定函数的定义域．（2）利用三角函数的倍角公式以及辅助角公式将函数进行化简，结合三角函数的最值性质求出矩形面积的最大值．以及利用向量数量积的定义进行求解即可．（3）根据几何概型的概率公式求出矩形PNMQ的面积y≥ 时，对应的角θ的取值范围，即可得到结论．
【考点精析】本题主要考查了几何概型的相关知识点，需要掌握几何概型的特点：1）试验中所有可能出现的结果（基本事件）有无限多个；2）每个基本事件出现的可能性相等才能正确解答此题．