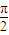题目内容
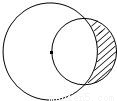
 如图,过半径为2的圆M上两点P、Q的切线相较于点T,自点P向平行于PQ的直径AB的两端各作一直线,这两条直线分别交垂直于PQ的直径所在直线于点R,S.试建立适当的直角坐标系用解析法证明:RT=ST.
如图,过半径为2的圆M上两点P、Q的切线相较于点T,自点P向平行于PQ的直径AB的两端各作一直线,这两条直线分别交垂直于PQ的直径所在直线于点R,S.试建立适当的直角坐标系用解析法证明:RT=ST.
分析:建立平面直角坐标系,写出圆的方程,设P坐标表示AP、BP的方程,求出R、S的横坐标,利用切线方程求出T的横坐标,分别求RT、ST即可.
解答:证明:如图,以圆心M为原点,平行于PQ的直径AB所在直线为y轴,建立平面直角坐标系
则可得圆的方程x2+y2=4,A(0,2)、B(0,-2),
设P(x0,y0),则x02+y02=4.
直线AP的方程为:y=
x+2,令y=0得xR=
,
直线BP的方程为:y=
x-2,令y=0得xS=
,
∵切线PT方程为x0x+y0y=4,由对称性知点T在x轴上,
故令y=0得xT=
∴RT=|xR-xT|=|
-
|=|
| = |
|.
ST=|xs-xT|=|
-
|=|
| = |
|,
∴RT=ST.
则可得圆的方程x2+y2=4,A(0,2)、B(0,-2),
设P(x0,y0),则x02+y02=4.
直线AP的方程为:y=
| y0-2 |
| x0 |
| 2x0 |
| 2-y0 |
直线BP的方程为:y=
| y0+2 |
| x0 |
| 2x0 |
| 2+y0 |
∵切线PT方程为x0x+y0y=4,由对称性知点T在x轴上,
故令y=0得xT=
| 4 |
| x0 |
∴RT=|xR-xT|=|
| 2x0 |
| 2-y0 |
| 4 |
| x0 |
| y0(2-y0) |
| (2-y0)x0 |
| y0 |
| x0 |
ST=|xs-xT|=|
| 2x0 |
| 2+y0 |
| 4 |
| x0 |
| y0(2+y0) |
| (2+y0)x0 |
| y0 |
| x0 |
∴RT=ST.
点评:本题考查直线和圆的方程的应用,解析法解决平面几何问题的关键在于建系,设点、表示距离,是中档题.

练习册系列答案
相关题目
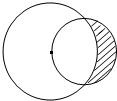 如图所示,一个半径为
如图所示,一个半径为| 2 |
| A、1 | ||
| B、2 | ||
C、
| ||
| D、4-π |
 (2011•成都二模)如图,在半径为l的球O中.AB、CD是两条互相垂直的直径,半径OP⊥平面ABCD.点E、F分别为大圆上的劣弧
(2011•成都二模)如图,在半径为l的球O中.AB、CD是两条互相垂直的直径,半径OP⊥平面ABCD.点E、F分别为大圆上的劣弧
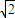 的圆过一个半径为2的圆的圆心,则图中阴影部分的面积为( )
的圆过一个半径为2的圆的圆心,则图中阴影部分的面积为( )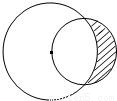
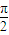
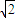 的圆过一个半径为2的圆的圆心,则图中阴影部分的面积为( )
的圆过一个半径为2的圆的圆心,则图中阴影部分的面积为( )