题目内容
已知函数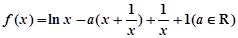 .
.
(Ⅰ)当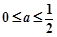 时,试讨论
时,试讨论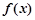 的单调性;
的单调性;
(Ⅱ)设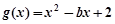 ,当
,当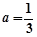 时,若对任意
时,若对任意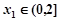 ,存在
,存在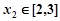 ,使
,使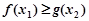 ,求实数
,求实数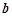 取值范围.
取值范围.
【答案】
(I) 当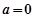 时,当
时,当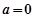 时,在
时,在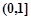 上,
上,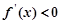 ,在
,在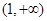 上,
上,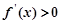 ,函数
,函数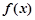 在
在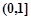 上单调递减,在
上单调递减,在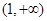 上单调递增;当
上单调递增;当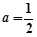 时,函数
时,函数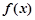 在
在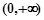 单调递减;当
单调递减;当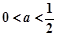 时,
时,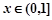 时,,函数
时,,函数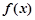 在
在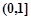 上单调递减;
上单调递减;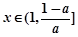 时,函数
时,函数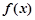 在
在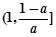 上单调递增;
上单调递增;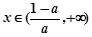 时,函数
时,函数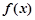 在
在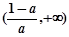 上单调递减;(II)实数
上单调递减;(II)实数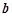 取值范围
取值范围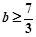 .
.
【解析】
试题分析:(I) 当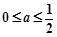 时,试讨论
时,试讨论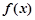 的单调性,首先确定定义域
的单调性,首先确定定义域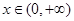 ,可通过单调性的定义,或求导确定单调性,由于
,可通过单调性的定义,或求导确定单调性,由于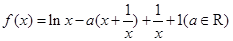 ,含有对数函数,可通过求导来确定单调区间,对函数
,含有对数函数,可通过求导来确定单调区间,对函数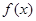 求导得
求导得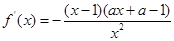 ,由此需对参数
,由此需对参数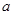 讨论,分
讨论,分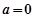 ,
,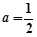 ,
,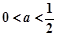 三种情况,判断导数的符号,从而得单调性;(II)设
三种情况,判断导数的符号,从而得单调性;(II)设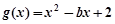 ,当
,当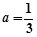 时,若对任意
时,若对任意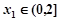 ,存在
,存在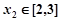 ,使
,使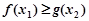 ,求实数
,求实数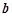 取值范围,由题意可知,当
取值范围,由题意可知,当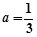 时,若对任意
时,若对任意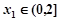 时,
时,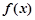 的最小值大于或等于当
的最小值大于或等于当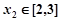 时
时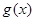 的最小值即可,由(I)知,当
的最小值即可,由(I)知,当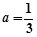 时,
时,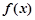 在
在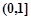 单调递减,在
单调递减,在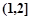 单调递增.
单调递增.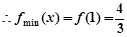 ,只需求出
,只需求出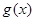 的最小值,由于本题属于对称轴不确定,需讨论,从而确定实数
的最小值,由于本题属于对称轴不确定,需讨论,从而确定实数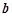 取值范围.也可用分离参数法来求.
取值范围.也可用分离参数法来求.
试题解析:(I)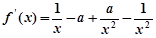 =
=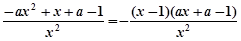 (
(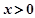 ) 3分
) 3分
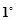 当
当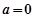 时,在
时,在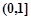 上,
上,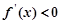 ,在
,在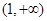 上,
上,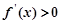 ,函数
,函数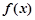 在
在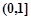 上单调递减,在
上单调递减,在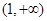 上单调递增; 4分
上单调递增; 4分
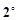 当
当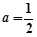 时,
时,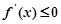 ,函数
,函数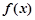 在
在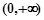 单调递减;
5分
单调递减;
5分
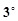 当
当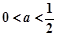 时,
时,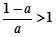 ,
,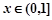 时,
时,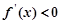 ,函数
,函数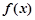 在
在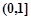 上单调递减;
上单调递减;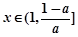 时,
时,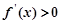 ,函数
,函数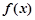 在
在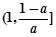 上单调递增;
上单调递增;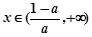 时,
时,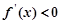 ,函数
,函数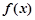 在
在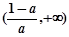 上单调递减. 7分
上单调递减. 7分
(II)若对任意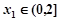 ,存在
,存在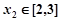 ,使
,使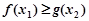 成立,只需
成立,只需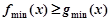 9分
9分
由(I)知,当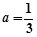 时,
时,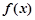 在
在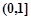 单调递减,在
单调递减,在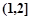 单调递增.
单调递增.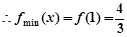 , 11分
, 11分
法一: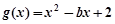 ,对称轴
,对称轴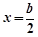 ,
,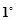 当
当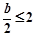 ,即
,即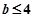 时,,得:
时,,得: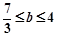 ;
;
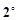 当
当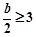 ,即
,即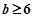 时,,得:
时,,得: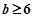 ;
;
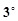 当
当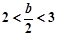 ,即
,即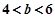 时,
时,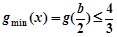 ,得:
,得: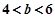 . 14分
. 14分
综上: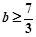 .
15分
.
15分
法二:
参变量分离: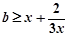 , 13分
, 13分
令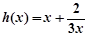 ,只需
,只需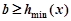 ,可知
,可知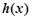 在
在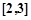 上单调递增,
上单调递增,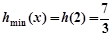 ,
,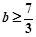 . 15分
. 15分
考点:函数与导数,函数单调性,存在解问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目