Question

若函数f（x）=x^a满足f（3）=9，那么函数g（x）=|log_a（x+1）|的图象大致为（　　）

• A、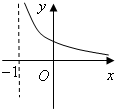
• B、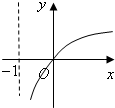
• C、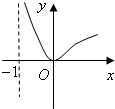
• D、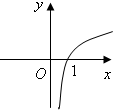

Answer 1

分析：利用f（3）=9，可得3^a=9，解得a=2．于是g（x）=|log₂（x+1）|=

log2(x+1)，x≥0 -log2(x+1)，-1＜x＜0

，分类讨论：当x≥0时，当-1＜x＜0时，函数g（x）单调性质，及g（0）=0即可得出．

解答：解：∵f（3）=9，
∴3^a=9，解得a=2．
∴g（x）=|log₂（x+1）|=

log2(x+1)，x≥0 -log2(x+1)，-1＜x＜0

，
∴当x≥0时，函数g（x）单调递增，且g（0）=0；当-1＜x＜0时，函数g（x）单调递减．
故选C．

点评：本题考查了幂函数的解析式、对数函数的单调性、分类讨论等基础知识与基本技能方法．