题目内容
已知椭圆 经过点M(-2,-1),离心率为
经过点M(-2,-1),离心率为 .过点M作倾斜角互补的两条直线分别与椭圆C交于异于M的另外两点P、Q.
.过点M作倾斜角互补的两条直线分别与椭圆C交于异于M的另外两点P、Q.
(I)求椭圆C的方程;
(II)试判断直线PQ的斜率是否为定值,证明你的结论.
(Ⅰ)解:由题设,∵椭圆 经过点M(-2,-1),离心率为
经过点M(-2,-1),离心率为 .
.
∴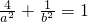 ,①且
,①且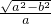 =
= ,②
,②
由①、②解得a2=6,b2=3,
∴椭圆C的方程为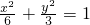 .…(6分)
.…(6分)
(Ⅱ)证明:记P(x1,y1)、Q(x2,y2).
设直线MP的方程为y+1=k(x+2),与椭圆C的方程联立,得(1+2k2)x2+(8k2-4k)x+8k2-8k-4=0,
∵-2,x1是该方程的两根,∴-2x1=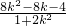 ,即x1=
,即x1=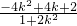 .
.
设直线MQ的方程为y+1=-k(x+2),同理得x2=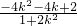 .…(9分)
.…(9分)
因y1+1=k(x1+2),y2+1=-k(x2+2),
故kPQ= =
=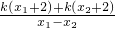 =
= =1,
=1,
因此直线PQ的斜率为定值.…(12分)
分析:(Ⅰ)根据椭圆 经过点M(-2,-1),离心率为
经过点M(-2,-1),离心率为 ,确定几何量之间的关系,即可求得椭圆C的方程;
,确定几何量之间的关系,即可求得椭圆C的方程;
(Ⅱ)记P(x1,y1)、Q(x2,y2),设直线MP的方程为y+1=k(x+2),与椭圆C的方程联立,求得x1=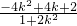 ,同理得x2=
,同理得x2=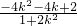 ,再利用kPQ=
,再利用kPQ= ,即可证得结论.
,即可证得结论.
点评:本题考查椭圆的标准方程,考查椭圆的几何性质,考查直线与椭圆的位置关系,确定椭圆的方程,联立方程组是关键.
 经过点M(-2,-1),离心率为
经过点M(-2,-1),离心率为 .
.∴
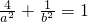 ,①且
,①且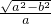 =
= ,②
,②由①、②解得a2=6,b2=3,
∴椭圆C的方程为
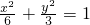 .…(6分)
.…(6分)(Ⅱ)证明:记P(x1,y1)、Q(x2,y2).
设直线MP的方程为y+1=k(x+2),与椭圆C的方程联立,得(1+2k2)x2+(8k2-4k)x+8k2-8k-4=0,
∵-2,x1是该方程的两根,∴-2x1=
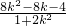 ,即x1=
,即x1=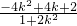 .
.设直线MQ的方程为y+1=-k(x+2),同理得x2=
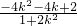 .…(9分)
.…(9分)因y1+1=k(x1+2),y2+1=-k(x2+2),
故kPQ=
 =
=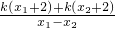 =
= =1,
=1,因此直线PQ的斜率为定值.…(12分)
分析:(Ⅰ)根据椭圆
 经过点M(-2,-1),离心率为
经过点M(-2,-1),离心率为 ,确定几何量之间的关系,即可求得椭圆C的方程;
,确定几何量之间的关系,即可求得椭圆C的方程;(Ⅱ)记P(x1,y1)、Q(x2,y2),设直线MP的方程为y+1=k(x+2),与椭圆C的方程联立,求得x1=
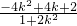 ,同理得x2=
,同理得x2=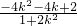 ,再利用kPQ=
,再利用kPQ= ,即可证得结论.
,即可证得结论.点评:本题考查椭圆的标准方程,考查椭圆的几何性质,考查直线与椭圆的位置关系,确定椭圆的方程,联立方程组是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
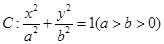 经过点M(-2,-1),离心率为
经过点M(-2,-1),离心率为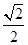 。过点M作倾斜角
。过点M作倾斜角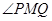 能否为直角?证明你的结论;
能否为直角?证明你的结论;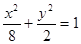 经过点M(2,1),O为坐标原点,平行于OM的直线l在y轴上的截距为m(m≠0)
经过点M(2,1),O为坐标原点,平行于OM的直线l在y轴上的截距为m(m≠0) 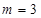 时,判断直线l与椭圆的位置关系;
时,判断直线l与椭圆的位置关系;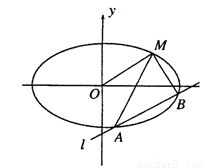
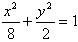 经过点M(2,1),O为坐标原点,平行于OM的直线l在y轴上的截距为m(m≠0),
经过点M(2,1),O为坐标原点,平行于OM的直线l在y轴上的截距为m(m≠0), 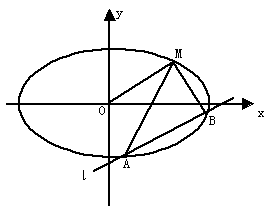
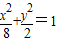 经过点M(2,1),O为坐标原点,平行于OM的直线l在y轴上的截距为m(m≠0).
经过点M(2,1),O为坐标原点,平行于OM的直线l在y轴上的截距为m(m≠0).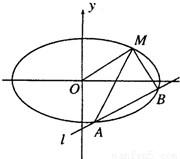
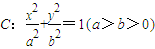 经过点M(-2,-1),离心率为
经过点M(-2,-1),离心率为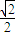 .过点M作倾斜角互补的两条直线分别与椭圆C交于异于M的另外两点P、Q.
.过点M作倾斜角互补的两条直线分别与椭圆C交于异于M的另外两点P、Q.