题目内容
若函数f(x)=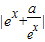 在
在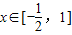 上增函数,则实数a的取值范围是 .
上增函数,则实数a的取值范围是 .
【答案】分析:分a<0和a≥0 两种情况进行讨论,当a<0时,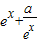 单调递增,则必有
单调递增,则必有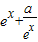 ≥0在
≥0在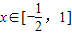 上恒成立;
上恒成立;
当a≥0时,f(x)=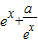 ,则有f′(x)=
,则有f′(x)=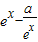 ≥0在
≥0在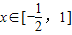 上恒成立,从而可求出a的取值范围.
上恒成立,从而可求出a的取值范围.
解答:解:(1)当a<0时,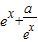 单调递增,
单调递增,
①若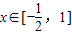 时,
时,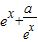 ≤0,则f(x)=-(
≤0,则f(x)=-(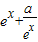 )单调递减,与函数f(x)=
)单调递减,与函数f(x)=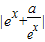 在
在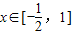 上是增函数不符;
上是增函数不符;
②若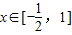 时,
时,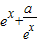 有零点x,
有零点x,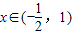 ,则-
,则- <x<x时,
<x<x时,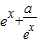 <0,f(x)=-(
<0,f(x)=-(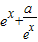 )单调递减,也与题意不符,
)单调递减,也与题意不符,
故必有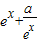 ≥0在
≥0在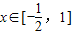 上恒成立,即a≥-e2x恒成立,
上恒成立,即a≥-e2x恒成立,
又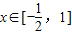 时,-e2x≤-
时,-e2x≤-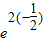 =-
=-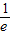 ,∴-
,∴-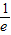 ≤a<0.
≤a<0.
(2)当a≥0时,f(x)=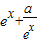 ,f′(x)=
,f′(x)=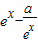 ,
,
∵f(x)在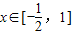 上是增函数,∴f′(x)=
上是增函数,∴f′(x)=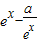 ≥0在
≥0在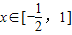 上恒成立,
上恒成立,
即a≤e2x,又e2x≥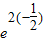 =
=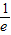 ,所以0<a≤
,所以0<a≤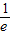 ,综上,实数a的取值范围为[-
,综上,实数a的取值范围为[-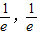 ].
].
故答案为:[-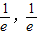 ].
].
点评:本题考查了函数的单调性,解决本题的难点在于函数解析式含有绝对值符号,故解决本题的关键在于去掉绝对值符号.
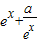 单调递增,则必有
单调递增,则必有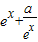 ≥0在
≥0在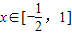 上恒成立;
上恒成立;当a≥0时,f(x)=
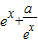 ,则有f′(x)=
,则有f′(x)=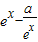 ≥0在
≥0在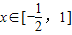 上恒成立,从而可求出a的取值范围.
上恒成立,从而可求出a的取值范围.解答:解:(1)当a<0时,
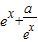 单调递增,
单调递增,①若
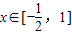 时,
时,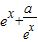 ≤0,则f(x)=-(
≤0,则f(x)=-(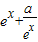 )单调递减,与函数f(x)=
)单调递减,与函数f(x)=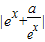 在
在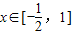 上是增函数不符;
上是增函数不符;②若
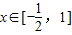 时,
时,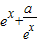 有零点x,
有零点x,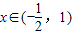 ,则-
,则- <x<x时,
<x<x时,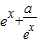 <0,f(x)=-(
<0,f(x)=-(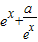 )单调递减,也与题意不符,
)单调递减,也与题意不符,故必有
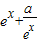 ≥0在
≥0在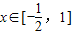 上恒成立,即a≥-e2x恒成立,
上恒成立,即a≥-e2x恒成立,又
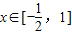 时,-e2x≤-
时,-e2x≤-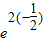 =-
=-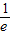 ,∴-
,∴-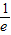 ≤a<0.
≤a<0.(2)当a≥0时,f(x)=
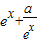 ,f′(x)=
,f′(x)=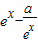 ,
,∵f(x)在
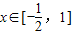 上是增函数,∴f′(x)=
上是增函数,∴f′(x)=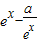 ≥0在
≥0在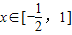 上恒成立,
上恒成立,即a≤e2x,又e2x≥
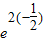 =
=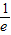 ,所以0<a≤
,所以0<a≤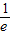 ,综上,实数a的取值范围为[-
,综上,实数a的取值范围为[-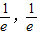 ].
].故答案为:[-
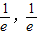 ].
].点评:本题考查了函数的单调性,解决本题的难点在于函数解析式含有绝对值符号,故解决本题的关键在于去掉绝对值符号.

练习册系列答案
相关题目