Question

已知函数f(x)=

mx3

3

+ax2+(1-b2)x，m，a，b∈R．
（Ⅰ）求函数f（x）的导函数f′（x）；
（Ⅱ）当m=1时，若函数f（x）是R上的增函数，求z=a+b的最小值；
（Ⅲ）当a=1，b=

2

时，函数f（x）在（2，+∞）上存在单调递增区间，求m的取值范围．

Answer 1

分析：（1）直接运用导数公式进行求导；
（2）根据函数f（x）是R上的增函数，转化成f'（x）≥0在R上恒成立．建立a，b的约束条件，利用参数方程求a+b的最小值；
（3）讨论m的范围，当m≥0时显然成立，当m＜0时，要使f'（x）在（2，+∞）上存在子区间使f'（x）＞0，应满足m＜0，
-

1

m

≥2，再结合图象建立不等关系即可．

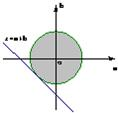解答：解：
（Ⅰ）f'（x）=mx²+2ax+（1-b²）．（3分）
（Ⅱ）因为函数f（x）是R上的增函数，所以f'（x）≥0在R上恒成立．
则有△=4a²-4（1-b²）≤0，即a²+b²≤1．
设

a=rcosθ b=rsinθ

（θ为参数，0≤r≤1），
则z=a+b=r（cosθ+sinθ）=

2

，sin(θ+

π

4

)．
当sin(θ+

π

4

)=-1，且r=1时，z=a+b取得最小值-

2

．
（Ⅲ）=1 ①当m＞0时，f'（x）=mx²+2x-1是开口向上的抛物线，
显然f'（x）在（2，+∞）上存在子区间使得f'（x）＞0，所以m的取值范围是（0，+∞）．
②当m=0时，显然成立．
③当m＜0时，f'（x）=mx²+2x-1是开口向下的抛物线，
要使f'（x）在（2，+∞）上存在子区间使f'（x）＞0，应满足m＜0，
-

1

m

≥2，
f′(-

1

m

)＞0，或

m＜0 - 1 m ＜2 f′(2)＞0

解得-

1

2

≤m＜0，或-

3

4

＜m＜-

1

2

，所以m的取值范围是(-

3

4

，0)．
则m的取值范围是(-

3

4

，+∞)．（13分）

点评：本题主要考查了导数的运算，以及利用导数研究函数的单调性和简单线性规划求最值，属于中档题．