题目内容
椭圆A.![]() B.
B.![]() C.
C.![]() D.4
D.4
解法一:(如下图)设椭圆的右焦点为F1,左焦点为F2,过F1垂直于x轴的直线与椭圆在第一象限的交点为P.
∵![]() +y2=1,
+y2=1,
∴a=2,b=1,c=![]() .
.
∴F1(![]() ,0).
,0).
设P(![]() ,yP),代入
,yP),代入![]() +y2=1,得yP=
+y2=1,得yP=![]() .
.
∴P(![]() ,
,![]() ),|PF1|=
),|PF1|=![]() .
.
又∵|PF2|+|PF1|=2a=4,
∴|PF2|=4-|PF1|=4-![]() =
=![]() .
.
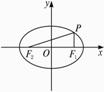
解法二:由解法一得P(![]() ,
,![]() ),又F2(
),又F2(![]() ,0),
,0),
∴|PF2|=![]() .
.
答案:C

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
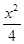 +y2=1的两个焦点,P是该椭圆上的一个动点, 则|PF1|·|PF2|的最大值是
.
+y2=1的两个焦点,P是该椭圆上的一个动点, 则|PF1|·|PF2|的最大值是
.