题目内容
【题目】各项均为正数的数列![]() 的前
的前![]() 项和为
项和为![]() ,且对任意正整数
,且对任意正整数![]() ,都有
,都有![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)如果等比数列![]() 共有2016项,其首项与公比均为2,在数列
共有2016项,其首项与公比均为2,在数列![]() 的每相邻两项
的每相邻两项![]() 与
与![]() 之间插入
之间插入![]() 个
个![]() 后,得到一个新的数列
后,得到一个新的数列![]() .求数列
.求数列![]() 中所有项的和;
中所有项的和;
(3)是否存在实数![]() ,使得存在
,使得存在![]() ,使不等式
,使不等式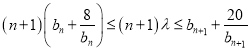 成立,若存在,求实数
成立,若存在,求实数![]() 的范围,若不存在,请说明理由.
的范围,若不存在,请说明理由.
【答案】(1)![]() (2)
(2)![]() (3)存在,
(3)存在,![]()
【解析】
(1)运用数列的通项和前![]() 项和的关系,结合等差数列的定义和通项公式,即可得到;
项和的关系,结合等差数列的定义和通项公式,即可得到;
(2)运用等比数列的求和公式和数列求和方法:分组求和,即可得到所求;
(3)运用参数分离可得![]() ,运用基本不等式和单调性,分别求出不等式左右两边的最值,即可得到所求范围.
,运用基本不等式和单调性,分别求出不等式左右两边的最值,即可得到所求范围.
解:(1)当![]() 时,由
时,由![]() 得
得![]() ,
,
当![]() 时,由
时,由![]() ,
,![]() 得
得
![]() ,
,
因数列![]() 的各项均为正数,所以
的各项均为正数,所以![]() ,
,
所以数列![]() 是首项与公差均为1的等差数列,
是首项与公差均为1的等差数列,
所以数列![]() 的通项公式为
的通项公式为![]() .
.
(2)数列![]() 的通项公式为
的通项公式为![]() .
.
数列![]() 中一共有
中一共有![]() 项,其所有项的和为
项,其所有项的和为
![]()
![]()
![]()
![]()
![]()
![]() .
.
(3) 由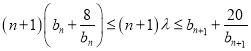 得
得
![]() ,
,![]() ,
,
记![]() ,
,![]() ,
,![]() ,
,
因为![]() ,当
,当![]() 取等号,所以
取等号,所以![]() 取不到
取不到![]() ,
,
当![]() 时,
时,![]() 的最小值为
的最小值为![]() ,
,
![]() 递减,
递减,![]() 的最大值为
的最大值为![]() .
.
所以如果存在![]() ,使不等式
,使不等式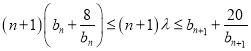 成立,
成立,
实数![]() 应满足
应满足![]() ,即实数
,即实数![]() 的范围应为
的范围应为![]() .
.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目