题目内容
设 是定义在
是定义在 上的函数,若
上的函数,若 ,且对任意
,且对任意 ,满足
,满足 ,
, ,则
,则 =( )
=( )
A. | B. | C. | D. |
D
解析试题分析:∵ ,∴
,∴ ∵
∵
∴ =
= ,即
,即
∵ ,∴
,∴ =
= ,∴
,∴ ,
,
∴
∴ =
= =
= = =
= = +
+  +
+ +
+ + +15•24+15•20="2008++"
+ +15•24+15•20="2008++"  +
+ +
+ + +15•24+15•20=
+ +15•24+15•20= =
= .
.
考点:不等式性质;叠加法;等比数列前n项和公式;函数的求值

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知{an}是公比为q的等比数列,且a1,a3,a2成等差数列,则q= ( ).
A.1或- | B.1 | C.- | D.-2[ |
已知正项等比数列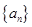 满足
满足 ,且
,且 ,则
,则 的最小值( )
的最小值( )
A. | B.2 | C.4 | D.6 |
如果-1,a,b,c,-9成等比数列,那么( )
| A.b=3,ac=9 | B.b=-3,ac=9 |
| C.b=3,ac=-9 | D.b=-3,ac=-9 |
设首项为l,公比为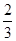 的等比数列
的等比数列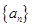 的前
的前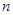 项和为
项和为 ,则 ( )
,则 ( )
A. | B.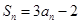 | C.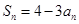 | D.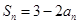 |
对任意等比数列 ,下列说法一定正确的是
,下列说法一定正确的是
A. 成等比数列 成等比数列 | B. 成等比数列 成等比数列 |
C. 成等比数列 成等比数列 | D. 成等比数列 成等比数列 |
(2013·大纲全国卷)已知数列{an}满足3an+1+an=0,a2=- ,则{an}的前10项和等于( )
,则{an}的前10项和等于( )
| A.-6(1-3-10) | B. (1-3-10) (1-3-10) |
| C.3(1-3-10) | D.3(1+3-10) |
 ,
, ,
,
 ;
; 时,求证:
时,求证:
 满足:
满足:

 满足:
满足: .
. ,求数列
,求数列 的前n项和
的前n项和 .
.