题目内容
已知正项等比数列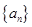 满足
满足 ,且
,且 ,则
,则 的最小值( )
的最小值( )
A. | B.2 | C.4 | D.6 |
C.
解析试题分析:∵正项等比数列 ,∴
,∴ ,
,
∴ 或
或 (舍去),∴
(舍去),∴ ,∴
,∴ ,
, ,∴
,∴ ,当且仅当
,当且仅当 时,等号成立,
时,等号成立,
∴ 的最小值是
的最小值是 .
.
考点:1.等比数列的性质;2.基本不等式求最值.

练习册系列答案
相关题目
等比数列 的前
的前 项和为
项和为 ,若
,若 ,
, ,则
,则 ( )
( )
| A.15 | B.30 | C.45 | D.60 |
一个等比数列 的前n项和为48,前2n项和为60,则前3n项和为( )
的前n项和为48,前2n项和为60,则前3n项和为( )
| A.63 | B.108 | C.75 | D.83 |
设 是定义在
是定义在 上的函数,若
上的函数,若 ,且对任意
,且对任意 ,满足
,满足 ,
, ,则
,则 =( )
=( )
A. | B. | C. | D. |
数列 的前
的前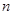 项和为
项和为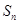 ,前
,前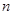 项积为
项积为 ,且
,且 ,则
,则 等于( )
等于( )
|
在等比数列{an}中,若a4,a8是方程x2-4x+3=0的两根,则a6的值是( )
A.- | B. | C.± | D.±3 |
在等比数列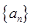 中,如果
中,如果 ,那么
,那么 等于( )
等于( )
| A.2 | B. | C. | D.4 |
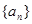 的前
的前 项和为
项和为 ,已知
,已知
 为等差数列,并写出
为等差数列,并写出 关于
关于 前
前 ,问满足
,问满足 的最小正整数
的最小正整数 的前
的前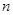 项和为
项和为 ,正数数列
,正数数列 的首项为
的首项为 ,
, .记数列
.记数列 前
前 .
. ,且
,且 ,使得
,使得 成等比数列?若存在,求出
成等比数列?若存在,求出