Question

已知数列的前项和，．

（1）求的通项公式；

（2）若对于任意的，有成立，求实数的取值范围．

Answer 1

解：（1）因为，，所以．

两式相减，得，即，

∴，．------------------------------------------------3分

又，即，所以．

∴是首项为3，公比为3的等比数列．----------------------------5分

从而的通项公式是，．--------------------------------6分

（2）由（1）知，对于任意的，有成立，

等价于对任意的成立，等价于．-----8分

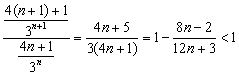而，，----------------10分

（注：也可以作差比较证明单调性，相应给分）

∴是单调递减数列．----------------------------------11分

∴，实数的取值范围是．-------------12分