题目内容
已知 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,若
,若 时有
时有
(Ⅰ)判断 在
在 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;
(Ⅱ)解不等式: ;
;
(Ⅲ)若 对所有
对所有 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
【答案】
解:(Ⅰ)任取 ,则
,则

∵ ,∴
,∴ , …………2分
, …………2分
由已知 >0,又
>0,又 ,
,
∴ ,即
,即 在
在 上为增函数. …………4分
上为增函数. …………4分
(Ⅱ) ∵ 在
在 上为增函数,故有
上为增函数,故有
 由此解得
由此解得 …………8分
…………8分
(Ⅲ)由(1)可知: 在
在 上是增函数,且
上是增函数,且 ,故对
,故对 ,恒有
,恒有 .所以要使
.所以要使 ,对所有
,对所有 ,
, 恒成立,
恒成立,
即要 成立,故
成立,故 成立. …………10分
成立. …………10分
记 对
对 ,
, 恒成立,只需
恒成立,只需 在
在 上的最小值大于等于零.故
上的最小值大于等于零.故
解得: 或
或 或
或 .
…………13分
.
…………13分
【解析】略

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,
, 的解析式;
的解析式; .
. 是定义在R上的奇函数,且
是定义在R上的奇函数,且 ,在[0,2]上
,在[0,2]上 ,则
,则 ;[来源:Z§xx§k.Com]
;[来源:Z§xx§k.Com] 且
且 ;
; 在[-8,8]内恰有四个不同的根
在[-8,8]内恰有四个不同的根 ,则
,则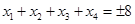 ;
;