题目内容
14.设函数$f(x)=sin(2x+\frac{π}{3})+\sqrt{3}-2\sqrt{3}{cos^2}$x.(1)求f(x)的最小正周期及其图象的对称中心;
(2)求函数f(x)的单调递增区间.
分析 (1)利用三角恒等变换化简函数的解析式,再利用正弦函数的周期性以及它的图象的对称性,求得f(x)的最小正周期及其图象的对称中心.
(2)利用正弦函数的单调性,求得函数f(x)的单调递增区间.
解答 解:(1)$f(x)=\frac{1}{2}sin2x+\frac{{\sqrt{3}}}{2}cos2x-\sqrt{3}cos2x$=$\frac{1}{2}sin2x-\frac{{\sqrt{3}}}{2}cos2x$=$sin({2x-\frac{π}{3}})$,
所以f(x)的最小正周期为$T=\frac{2π}{2}=π$.
令$2x-\frac{π}{3}=kπ({k∈Z})$,求得x=$\frac{kπ}{2}$+$\frac{π}{6}$,可得函数的图象对称中心为$({\frac{kπ}{2}+\frac{π}{6},0})({k∈Z})$.
(2)令$2kπ-\frac{π}{2}≤2x-\frac{π}{3}≤2kπ+\frac{π}{2}({k∈Z})$,解得$kπ-\frac{π}{12}≤x≤kπ+\frac{5π}{12}({k∈Z})$,
所以f(x)的单调递增区间为$[{kπ-\frac{π}{12},kπ+\frac{5π}{12}}]({k∈Z})$.
点评 本题主要考查三角恒等变换,正弦函数的周期性和单调性,以及它的图象的对称性,属于中档题.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
9.在正棱柱ABC-A1B1C1中,D是AC的中点,AA1:AB=$\sqrt{2}$:1,则异面直线AB1与BD所成的角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
19.sin$\frac{2017π}{3}$的值等于( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $-\frac{\sqrt{3}}{2}$ |
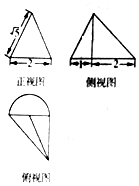 某几何体上的三视图如图所示,则该几何体的体积是$\frac{4+π}{3}$.
某几何体上的三视图如图所示,则该几何体的体积是$\frac{4+π}{3}$.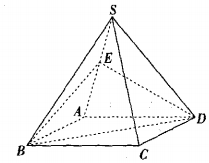 如图,四棱锥S-ABCD中,底面ABCD为平行四边形,E是SA的上一点,当点E满足条件SE=EA,时,SC∥平面EBD,写出条件并加以证明.
如图,四棱锥S-ABCD中,底面ABCD为平行四边形,E是SA的上一点,当点E满足条件SE=EA,时,SC∥平面EBD,写出条件并加以证明.