题目内容
两异面直线AB、CD都平行于平面α,M、N分别为AC、BD的中点,且M∈α,N∈α,设AB+CD=l,则有( )
分析:连接AD交平面α于点G,连接MG、NG,根据线面平行的性质定理,可得GN、GM分别是△ABD和△ACD的中位线.因为△MNG中,GM+GN>MN,所以
(AB+CD)>MN,由此即可得到本题的答案.
| 1 |
| 2 |
解答: 解:连接AD交平面α于点G,连接MG、NG
解:连接AD交平面α于点G,连接MG、NG
∵AB∥平面α,AB?平面ABD,平面ABD∩平面α=GN
∴GN∥AB
∵△ABD中,N是BD中点,
∴GN是△ABD的中位线,可得GN=
AB
同理,可得GM是△ACD的中位线,可得GM=
CD
∵直线AB、CD是异面直线
∴M、N、G三点不共线
故△MNG中,GM+GN>MN,即
(AB+CD)>MN,
∵AB+CD=l,∴MN<
l
故选:B
 解:连接AD交平面α于点G,连接MG、NG
解:连接AD交平面α于点G,连接MG、NG∵AB∥平面α,AB?平面ABD,平面ABD∩平面α=GN
∴GN∥AB
∵△ABD中,N是BD中点,
∴GN是△ABD的中位线,可得GN=
| 1 |
| 2 |
同理,可得GM是△ACD的中位线,可得GM=
| 1 |
| 2 |
∵直线AB、CD是异面直线
∴M、N、G三点不共线
故△MNG中,GM+GN>MN,即
| 1 |
| 2 |
∵AB+CD=l,∴MN<
| 1 |
| 2 |
故选:B
点评:本题给出与平面α平行且在平面α两侧的异面线段AB、CD,在已知AC、BD交平面α于M、N的情况下比较
(AB+CD)与MN的大小,着重考查了直线与平面平行的性质定理、三角形的中位线等知识,属于基础题.
| 1 |
| 2 |

练习册系列答案
相关题目
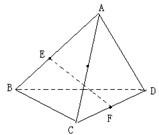 如图,在四面体ABCD中,已知所有棱长都为a,点E、F分别是AB、CD的中点.
如图,在四面体ABCD中,已知所有棱长都为a,点E、F分别是AB、CD的中点. (1)求线段EF的长;(EF是两异面直线AB与CD的公垂线);
(1)求线段EF的长;(EF是两异面直线AB与CD的公垂线);  如图,在四面体ABCD中,已知所有棱长都为a,点E、F分别是AB、CD的中点.
如图,在四面体ABCD中,已知所有棱长都为a,点E、F分别是AB、CD的中点.