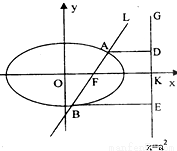
题目内容
 如图,已知直线L:
如图,已知直线L: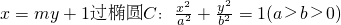 的右焦点F,且交椭圆C于A、B两点,点A、B在直线G:x=a2上的射影依次为点D、E.
的右焦点F,且交椭圆C于A、B两点,点A、B在直线G:x=a2上的射影依次为点D、E.
(1)若抛物线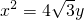 的焦点为椭圆C的上顶点,求椭圆C的方程;
的焦点为椭圆C的上顶点,求椭圆C的方程;
(2)若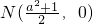 为x轴上一点,求证:
为x轴上一点,求证: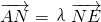 .
.
解:由题意,已知直线L: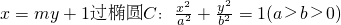 的右焦点F,故有c=1
的右焦点F,故有c=1
(1)抛物线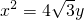 的焦点为(0,
的焦点为(0, )故椭圆C的上顶点的坐标为(0,
)故椭圆C的上顶点的坐标为(0, ),可得b=
),可得b= ,由椭圆的性质得a=2
,由椭圆的性质得a=2
故椭圆C的方程为
(2)设A(x1,y1)B(x2,y2)E(a2,y2)D(a2,y1)
当m变化时首先AE过定点N
 即(a2+b2m2)y2+2mb2y+b2(1-a2)=0
即(a2+b2m2)y2+2mb2y+b2(1-a2)=0
△=4a2b2(a2+m2b2-1)>0(a>1)



∵
 =
=
∴kAN=KEN
∴A、N、E三点共线
∴故存在实数λ使得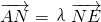 .
.
分析:(1)易知 ,c=1,结合a2=b2+c2可求椭圆的方程
,c=1,结合a2=b2+c2可求椭圆的方程
(2)要证当m变化时,直线AE、BD相交于一定点.先找m去特殊值(m=0)时AE与BD相交FK中点 故猜想:当m变化时,AE与BD相交于定点
故猜想:当m变化时,AE与BD相交于定点  然后只要证明AN,EN 的斜率相等,从而可得A、N、E三点共线同理可得B、N、D三点共线即可
然后只要证明AN,EN 的斜率相等,从而可得A、N、E三点共线同理可得B、N、D三点共线即可
点评:本题主要考查了圆锥曲线的性质的综合应用,而定义的灵活应用是解决本题的关键直线与曲线的相交的一般思路是联立方程组,通过方程的根与系数的关系进行求解,本题符号运算,较繁,变形时要严谨.
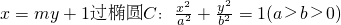 的右焦点F,故有c=1
的右焦点F,故有c=1(1)抛物线
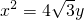 的焦点为(0,
的焦点为(0, )故椭圆C的上顶点的坐标为(0,
)故椭圆C的上顶点的坐标为(0, ),可得b=
),可得b= ,由椭圆的性质得a=2
,由椭圆的性质得a=2故椭圆C的方程为

(2)设A(x1,y1)B(x2,y2)E(a2,y2)D(a2,y1)
当m变化时首先AE过定点N
 即(a2+b2m2)y2+2mb2y+b2(1-a2)=0
即(a2+b2m2)y2+2mb2y+b2(1-a2)=0△=4a2b2(a2+m2b2-1)>0(a>1)



∵

 =
=
∴kAN=KEN
∴A、N、E三点共线
∴故存在实数λ使得
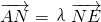 .
.分析:(1)易知
 ,c=1,结合a2=b2+c2可求椭圆的方程
,c=1,结合a2=b2+c2可求椭圆的方程(2)要证当m变化时,直线AE、BD相交于一定点.先找m去特殊值(m=0)时AE与BD相交FK中点
 故猜想:当m变化时,AE与BD相交于定点
故猜想:当m变化时,AE与BD相交于定点  然后只要证明AN,EN 的斜率相等,从而可得A、N、E三点共线同理可得B、N、D三点共线即可
然后只要证明AN,EN 的斜率相等,从而可得A、N、E三点共线同理可得B、N、D三点共线即可点评:本题主要考查了圆锥曲线的性质的综合应用,而定义的灵活应用是解决本题的关键直线与曲线的相交的一般思路是联立方程组,通过方程的根与系数的关系进行求解,本题符号运算,较繁,变形时要严谨.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目

 如图,已知直线L:
如图,已知直线L: 的右焦点F,且交椭圆C于A、B两点,点A、B在直线G:x=a2上的射影依次为点D、E.
的右焦点F,且交椭圆C于A、B两点,点A、B在直线G:x=a2上的射影依次为点D、E. 的焦点为椭圆C 的上顶点,求椭圆C的方程;(2)(理科生做)连接AE、BD,试探索当m变化时,直线AE、BD是否相交于一定点N?若交于定点N,请求出N点的坐标,并给予证明;
的焦点为椭圆C 的上顶点,求椭圆C的方程;(2)(理科生做)连接AE、BD,试探索当m变化时,直线AE、BD是否相交于一定点N?若交于定点N,请求出N点的坐标,并给予证明; 为x轴上一点,求证:
为x轴上一点,求证: .
.
 的右焦点F,且交椭圆C于A、B两点,点A、B在直线G:x=a2上的射影依次为点D、E.
的右焦点F,且交椭圆C于A、B两点,点A、B在直线G:x=a2上的射影依次为点D、E. 的焦点为椭圆C的上顶点,求椭圆C的方程;
的焦点为椭圆C的上顶点,求椭圆C的方程; 为x轴上一点,求证:
为x轴上一点,求证: .
.