题目内容

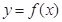定义域为[]的函数图像的两个端点为A、B，M(x，y)是图象上任意一点，其中．已知向量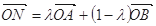，若不等式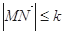恒成立， 则称函数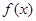在[]上“k阶线性近似”．若函数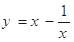在[1，2]上“k阶线性近似”，则实数k的取值范围为(     )

A．[0，+∞)          B．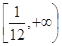

C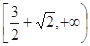．    D．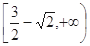

 

【答案】

D

【解析】

试题分析：由题意，M、N横坐标相等，|

||≤k恒成立即k恒大于等于||，则k≥||的最大值，所以本题即求||的最大值．

由N在AB线段上，得A（1，0），B（2，），AB方程y=（x-1）

由图象可知，MN=y1-y2=x--（x-1）=-（+）≤-

（均值不等式）

故选D．

考点：本题主要考查向量的线性运算，新定义问题，均值定理的应用。

点评：求解的关键是理解题意并得出M、N横坐标相等，将恒成立问题转化为求函数的最值问题．

 

练习册系列答案
相关题目
精英家教网设定义域为R的函数f(x)=
|x+1|，x≤0
(x-1)2，x＞0
．
（1）在平面直角坐标系内作出该函数的图象；
（2）试找出一组b和c的值，使得关于x的方程f2（x）+b•f（x）+c=0有7个不同的实根．请说明你的理由．
12、已知定义域为R的函数y=f（x），则下列命题：
①若f（x-1）=f（1-x）恒成立，则函数y=f（x）的图象关于直线x=1的对称；
②若f（x+1）+f（1-x）=0恒成立，则函数y=f（x）的图象关于（1，0）点对称；
③函数y=f（x-1）的图象与函数y=f（1-x）的图象关于y轴对称；
④函数y=-f（x-1）的图象与函数y=f（1-x）的图象关于原点对称；
⑤若f（1+x）+f（x-1）=0恒成立，则函数y=f（x）以4为周期．
其中真命题的有（　　）
设定义域为R的函数f（x），g（x）都有反函数，g（x）的反函数为h（x），令u（x）=f（x-1），v（x）=h（x-3），可得函数u（x）和v（x）图象关于直线y=x对称，若g（5）=2005，则f（4）等于（　　）
（2013•荆门模拟）下列命题中正确的是
①②③
①②③
．
①如果幂函数y=(m2-3m+3)xm2-m-2的图象不过原点，则m=1或m=2；
②定义域为R的函数一定可以表示成一个奇函数与一个偶函数的和；
③已知直线a、b、c两两异面，则与a、b、c同时相交的直线有无数条；
④方程
y-3
x-2
=
y-1
x+3
表示经过点A（2，3）、B（-3，1）的直线；
⑤方程
x2
2+m
-
y2
m+1
=1表示的曲线不可能是椭圆．
设定义域为R的函数f（x），g（x）都有反函数，且函数f（x-1）和g-1（x-3）图象关于直线y=x对称，若g（5）=2005，则f（4）为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网