Question

设定义域为R的函数f(x)=

|x+1|，x≤0 (x-1)2，x＞0

．
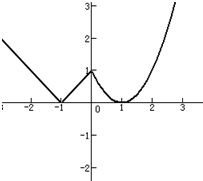
（1）在平面直角坐标系内作出该函数的图象；
（2）试找出一组b和c的值，使得关于x的方程f²（x）+b•f（x）+c=0有7个不同的实根．请说明你的理由．

Answer 1

分析：（1）根据分段函数图象分段画的原则，结合绝对值函数的性质及二次函数的性质，我们易画出函数的图象；
（2）本题是一个开放题，没有固定的答案，使得关于x的方程f²（x）+b•f（x）+c=0有7个不同的实根，则f（x）=1有3个解，f（x）=a∈（0，1）有四个解，只要列出b和c的值，能够满足条件即可．

解答：解：（1）如下图所示：

（2）b=-

3

2

，c=

1

2

满足条件，理由如下：
设f（x）=t，t²+bt+c=0，
由图象可得以上有关于t的方程必须有一解为1，
另一解在区间（0，1）中，
才会使得关于x的方程f²（x）+b•f（x）+c=0有7个解．
其中，f（x）=1有3个解，
f（x）=a∈（0，1）有四个解．
所以可令t1=1，t2=

1

2

，
即可得方程x2-

3

2

x+

1

2

=0．

点评：本题考查的知识点是根的存在性及根的个数判断及函数的图象，其中根据绝对值函数的性质及二次函数的性质，画出函数的图象并结合函数图象即可得到答案．