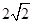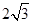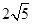题目内容
设 是椭圆
是椭圆 的左、右焦点,
的左、右焦点,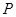 为直线
为直线 上一点,
上一点,
 是底角为
是底角为 的等腰三角形,则
的等腰三角形,则 的离心率为( )
的离心率为( )
A. | B. | C. | D. |

C
解析试题分析:因为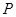 为直线
为直线 上一点,
上一点,
 是底角
是底角
为 的等腰三角形,
的等腰三角形, 所以
所以 ,
,
又因为 所以
所以 解得离心率为
解得离心率为
考点:本小题主要考查椭圆中基本量和边角关系的计算,考查学生基础知识的运用能力.
点评:椭圆是常考题目,但是与椭圆有关的题目一般运算量比较大,这时画出图象辅助答题有时可以简化运算,使题目变得简单.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
已知点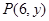 在抛物线
在抛物线 上,
上, 为抛物线焦点, 若
为抛物线焦点, 若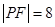 , 则点
, 则点 到抛物线准线的距离等于( )
到抛物线准线的距离等于( )
| A.2 | B.1 | C.4 | D.8 |
设点 是曲线
是曲线 上的点,
上的点, ,则( )
,则( )
A. | B. |
C. | D. |
椭圆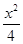 +
+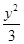 =1的右焦点到直线y=
=1的右焦点到直线y= x的距离是 ( )
x的距离是 ( )
A.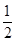 | B.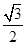 | C.1 | D. |
已知双曲线 的一个焦点与抛物线
的一个焦点与抛物线
的焦点重合,且双曲线的离心率等于 ,则该双曲线的标准方程为( )
,则该双曲线的标准方程为( )
A. | B. |
C. | D. |
抛物线 的焦点坐标是( )
的焦点坐标是( )
A. | B. | C.  | D. |
设定点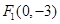 、
、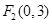 ,动点
,动点 满足条件
满足条件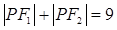 ,则点
,则点 的轨迹是( )
的轨迹是( )
| A.椭圆 | B.线段 | C.不存在 | D.线段或椭圆 |
若抛物线的准线方程为x=–7, 则抛物线的标准方程为( )
| A.x2=–28y | B.y2=28x |
| C.y2=–28x | D.x2=28y |
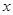 轴对称,它的顶点在坐标原点
轴对称,它的顶点在坐标原点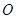 ,并且经过点
,并且经过点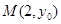 .若点
.若点 到该抛物线焦点的距离为
到该抛物线焦点的距离为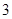 ,则
,则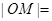 ( )
( )