题目内容
已知角A是△ABC的内角,向量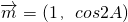 ,
,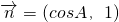 ,且
,且 ,
, ,
,
(Ⅰ)求角A的大小;
(Ⅱ)求函数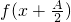 的单调递增区间.
的单调递增区间.
解:(Ⅰ)∵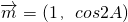 ,
,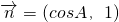 ,且
,且 ,
,
∴cosA+cos2A=0?2cos2A+cosA-1=0,(2分)
∴ 或cosA=-1,(4分)
或cosA=-1,(4分)
∵角A是△ABC的内角,∴0<A<π,
∴ (6分)
(6分)
(Ⅱ)∵ (8分)
(8分)
∴ (9分)
(9分)
由 2kπ- ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,
,
得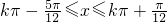 ,k∈Z(11分)
,k∈Z(11分)
∴函数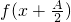 的单调递增区间为
的单调递增区间为 k∈Z(12分)
k∈Z(12分)
分析:(Ⅰ)由 ,求出cosA的值,再由cosA的值确定角A的大小.
,求出cosA的值,再由cosA的值确定角A的大小.
(Ⅱ)化简函数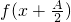 的解析式到 2sin(2x+
的解析式到 2sin(2x+ ),利用正弦函数的单调增区间,
),利用正弦函数的单调增区间,
求出此函数的单调区间,即由 2kπ- ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,解出x的范围,即得
,解出x的范围,即得
函数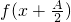 的单调增区间.
的单调增区间.
点评:本题考查平面向量的数量积的运算,两角和与差的三角函数,正弦函数的单调增区间[2kπ- ,2kπ+
,2kπ+ ].
].
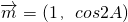 ,
,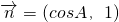 ,且
,且 ,
,∴cosA+cos2A=0?2cos2A+cosA-1=0,(2分)
∴
 或cosA=-1,(4分)
或cosA=-1,(4分)∵角A是△ABC的内角,∴0<A<π,
∴
 (6分)
(6分)(Ⅱ)∵
 (8分)
(8分)∴
 (9分)
(9分)由 2kπ-
 ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,
,得
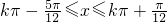 ,k∈Z(11分)
,k∈Z(11分)∴函数
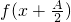 的单调递增区间为
的单调递增区间为 k∈Z(12分)
k∈Z(12分)分析:(Ⅰ)由
 ,求出cosA的值,再由cosA的值确定角A的大小.
,求出cosA的值,再由cosA的值确定角A的大小.(Ⅱ)化简函数
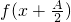 的解析式到 2sin(2x+
的解析式到 2sin(2x+ ),利用正弦函数的单调增区间,
),利用正弦函数的单调增区间,求出此函数的单调区间,即由 2kπ-
 ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,解出x的范围,即得
,解出x的范围,即得函数
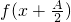 的单调增区间.
的单调增区间.点评:本题考查平面向量的数量积的运算,两角和与差的三角函数,正弦函数的单调增区间[2kπ-
 ,2kπ+
,2kπ+ ].
]. 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
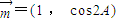 ,
,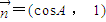 ,且
,且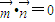 ,
,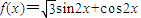 ,
,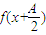 的单调递增区间.
的单调递增区间.