题目内容
已知函数 是定义在
是定义在 上的偶函数,且
上的偶函数,且 时,
时, ,函数
,函数 的值域为集合
的值域为集合 .
.
(I)求 的值;
的值;
(II)设函数 的定义域为集合
的定义域为集合 ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围.
(I) ;(II)
;(II) .
.
解析试题分析:(I)因为函数 是定义在
是定义在 上的偶函数,
上的偶函数,
(II)由函数 是定义在
是定义在 上的偶函数,可得函数
上的偶函数,可得函数 的值域
的值域 即为
即为 时,
时, 的取值范围.
的取值范围.
又 .
.
由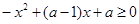 得
得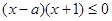 .
.
再由 可得实数
可得实数 的取值范围是.
的取值范围是.
试题解析:(I)  函数
函数 是定义在
是定义在 上的偶函数,
上的偶函数, 1分
1分
又  时,
时,
 2分
2分 3分
3分
(II)因为函数 是定义在
是定义在 上的偶函数,
上的偶函数,
所以函数 的值域
的值域 即为
即为 时,
时, 的取值范围. 5分
的取值范围. 5分
当 时,
时,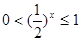 7分
7分
故函数 的值域
的值域 =
= . 8分
. 8分 ,
, 定义域
定义域 . 9分
. 9分
由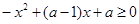 得
得 ,
,
即 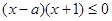 . 10分
. 10分
 ,
, 且
且 ,
, 实数
实数 的取值范围是
的取值范围是 . 12分
. 12分
考点:1、函数的奇偶性;2、函数的定义域和值域;3、集合的基本运算.

练习册系列答案
相关题目
 。
。 且对任意实数
且对任意实数 均有
均有 成立,求
成立,求 的表达式;
的表达式; 时,
时, 是单调函数,求实数
是单调函数,求实数 的取值范围.
的取值范围. .已知甲、乙两地相距100千米.
.已知甲、乙两地相距100千米. .
. 时,画出函数
时,画出函数 的简图,并指出
的简图,并指出 (其中
(其中 )的图象如图所示.
)的图象如图所示.
 的解析式;
的解析式; ,且
,且 ,求
,求 的单调区间.
的单调区间. ,其中
,其中
 的奇偶性与单调性(不要求证明);
的奇偶性与单调性(不要求证明); 的定义域为
的定义域为 ,求满足不等式
,求满足不等式 的实数
的实数 的取值集合;
的取值集合; 时,
时, 的值恒为负,求
的值恒为负,求 的取值范围.
的取值范围. 对任意
对任意 满足
满足 ,
, ,若当
,若当 时,
时, (
( 且
且 ),且
),且 .
. 的值;
的值; 的值域.
的值域. .
. ,解不等式
,解不等式 ;
; ,
, ,求实数
,求实数 的取值范围.
的取值范围. 的定义域是
的定义域是 ,
, 是
是 在
在 的单调区间;
的单调区间; ,求
,求 的取值范围;
的取值范围; 是
是 ,求证:
,求证: .
.