Question

如图，在棱长为1的正方体ABCD-A₁B₁C₁D₁中，点E是棱BC的中点，点F是棱CD的中点．

(1)求证D₁E⊥平面AB₁F；

(2)求二面角G₁-EF-A的大小(结果用反三角函数值表示)．

Answer 1

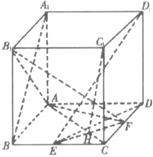
解：(1)连结A_lB，则D₁E在侧面ABB₁A₁上的射影是A₁B，又∵A₁B⊥AB₁，∴D₁E⊥AB₁，

连结DE，∵D₁E在底面ABCD上的射影是DE，E、F均为中点，

∴DE⊥AF，∴D₁E⊥AF

∴D₁E⊥平面AB₁F

(2)∵C₁C⊥平面EFA，连结AC交EF于H，则AH⊥EF，

连结C₁H，则C₁H在底面ABCD上的射影是CH，

∴C₁H⊥EF，

∴∠C₁HA为二面角C₁-EF-A的平面角，它是∠C₁HC的邻补角．

在Rt△C₁CH中，∵C₁C=1，CH=AC=，

∴tan∠C₁HC=．

∴∠C₁HC=arctan2，

∴∠C₁HA=π-arctan2

另解：(1)以A为坐标原点，建立如图所示的空间直角坐标系．

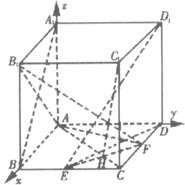
则A(0，0，0)，B(1，0，0)，D(0，1，0)，A₁(0，0，1)，B₁(1，0，1)，E(1，，0)，F(，1，0)，D_l(0，1，1)．

∴=(1，，-1)，=(1，0，1)

∴·=1-1=0，∴D₁E⊥AB₁

又=(，1，0)，

∴·=-=0，∴D₁E⊥AF．

∴D₁E⊥平面AB₁F

(2)∵C₁C⊥平面EFA，连结AC交EF于H，则AH⊥EF，C₁H在底面ABCD上的射影是CH，∴C₁H⊥EF

∴∠C₁HA为二面角C₁-EF-A的平面角．

∵C₁(1，1，1)，H(，0)

∴=(,,1)，=(，,0)

cos＜,＞=

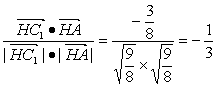
∴∠C₁HA =π-arccos