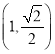题目内容
【题目】若数列
同时满足：①对于任意的正整数
， 
恒成立；②对于给定的正整数
， 
对于任意的正整数
恒成立，则称数列
是“
数列”.
（1）已知
判断数列
是否为“
数列”，并说明理由；
（2）已知数列
是“
数列”，且存在整数
，使得
， 
， 
， 
成等差数列，证明： 
是等差数列.
【答案】（1）是（2）见解析
【解析】试题分析：（1）根据定义验证两个条件是否成立，由于函数为分段函数，所以分奇偶分别验证（2）根据定义数列隔项成等差，再根据单调性确定公差相等，最后求各项通项，根据通项关系得数列
通项，根据等差数列证结论
试题解析：（1）当
为奇数时， 
，所以
.
.
当
为偶数时， 
，所以
.
.
所以，数列
是“
数列”.
（2）由题意可得： 
，
则数列
， 
， 
， 
是等差数列，设其公差为
，
数列
， 
， 
， 
是等差数列，设其公差为
，
数列
， 
， 
， 
是等差数列，设其公差为
.
因为
，所以
，
所以
，
所以
①，
②.
若
，则当
时，①不成立；
若
，则当
时，②不成立；
若
，则①和②都成立，所以
.
同理得： 
，所以
，记
.
设
，
则
.
同理可得： 
，所以
.
所以
是等差数列.
【另解】
，
，
，
以上三式相加可得： 
，所以
，
所以
，
，
，
所以
，所以
，
所以，数列
是等差数列.
练习册系列答案
相关题目
