题目内容
设函数
（1）求
的单调区间、最大值；
（2）讨论关于
的方程
的根的个数．
解：（1）
………………1分
由
得
当
时，
，单调递增；
当
时，
，单调递减；
∴函数的单调递增区间是
；单调递减区间是
…………3分
∴的最大值为
…………4分
（2）令
＝
…………5分
①当
时，
∴
∵
∴
∴
在上单调递增 ………………7分
②当
时，
，
∵
∴
∴在（0,1）上单调递减
综合①②可知，当
时，
…………9分
当
即
时，没有零点，故关于方程
的根的个数为0
当
即
时，只有一个零点，故关于方程的根的个数为1
……………………11分
当
即
时，当时
由（1）知
要使
，只需
即
当时， 由(1)知
要使
，只需
即
所以时，有两个零点 ………………13分
综上所述
当时，关于的方程
根的个数为0
当
时，关于的方程根的个数为1
当
时，关于的方程根的个数为2 …………14分
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
的单调增区间和单调减区间；
时（其中e=2.71828…），不等式
恒成立，求实数m的取值范围；
上恰有两个相异的实根，求实数a的取值范围。
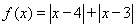
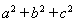
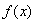
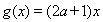
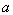
的值； （2）若
，求
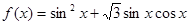
的最小正周期和值域;
的图象按向量
平移后得到函数
的图
象，求函数