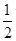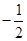题目内容
已知数列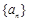 的前
的前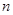 项和
项和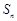 满足:
满足: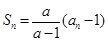 (
(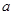 为常数,且
为常数,且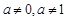 ).
).
(1)求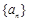 的通项公式;
的通项公式;
(2)设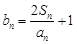 ,若数列
,若数列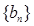 为等比数列,求
为等比数列,求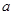 的值;
的值;
(3)在满足条件(2)的情形下,设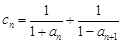 ,数列
,数列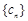 的前
的前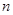 项和为
项和为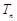 ,求证:
,求证: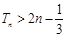 .
.
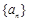 的前
的前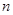 项和
项和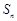 满足:
满足: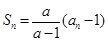 (
(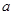 为常数,且
为常数,且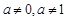 ).
). (1)求
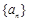 的通项公式;
的通项公式;(2)设
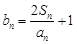 ,若数列
,若数列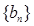 为等比数列,求
为等比数列,求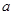 的值;
的值;(3)在满足条件(2)的情形下,设
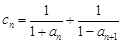 ,数列
,数列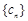 的前
的前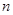 项和为
项和为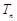 ,求证:
,求证: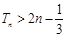 .
.(1)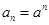 ;(2)
;(2)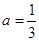 ;(3)证明过程详见解析.
;(3)证明过程详见解析.
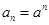 ;(2)
;(2)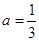 ;(3)证明过程详见解析.
;(3)证明过程详见解析.试题分析:本题主要考查数列的通项公式和数列求和问题,考查学生的计算能力和分析问题的能力以及推理论证的能力.第一问,是由
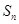 求
求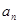 ;第二问,先把第一问的结论代入,整理出
;第二问,先把第一问的结论代入,整理出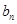 表达式,已知
表达式,已知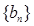 为等比数列,所以用数列的前3项的关系列式求
为等比数列,所以用数列的前3项的关系列式求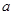 ;第三问,把第二问的结果代入,化简
;第三问,把第二问的结果代入,化简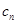 表达式,本问应用了放缩法和分组求和的方法.
表达式,本问应用了放缩法和分组求和的方法.试题解析:(1)
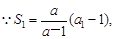 ∴
∴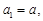
当
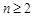 时,
时,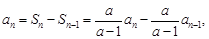
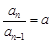 ,即
,即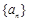 是等比数列. ∴
是等比数列. ∴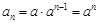 ; 4分
; 4分(2)由(Ⅰ)知,
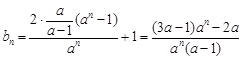 ,若
,若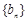 为等比数列,
为等比数列,则有
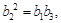 而
而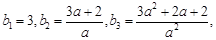
故
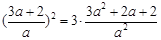 ,解得
,解得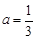 , 7分
, 7分再将
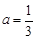 代入得
代入得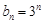 成立, 所以
成立, 所以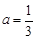 . 8分
. 8分(3)证明:由(Ⅱ)知
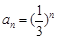 ,所以
,所以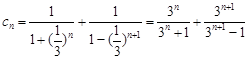

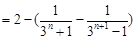 , 9分
, 9分由
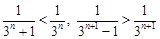 得
得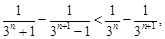
所以
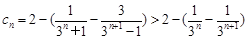 , 12分
, 12分从而
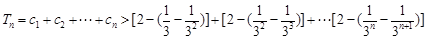
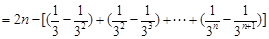
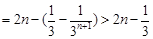 .
.即
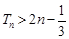 . 14分
. 14分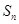 求
求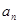 ;2.等比数列的通项公式;3.等比中项;4.放缩法;5.分组求和.
;2.等比数列的通项公式;3.等比中项;4.放缩法;5.分组求和.
练习册系列答案
相关题目
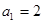 ,点
,点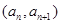 在函数
在函数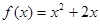 的图像上,(其中
的图像上,(其中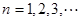 )
)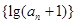 是等比数列;
是等比数列;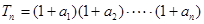 ,求
,求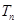 及数列
及数列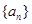 的通项.
的通项.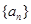 满足公比
满足公比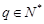 ,
,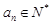 ,且{
,且{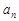 }中的任意两项之积也是该数列中的一项,若
}中的任意两项之积也是该数列中的一项,若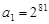 ,则
,则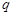 的所有可能取值的集合为 .
的所有可能取值的集合为 .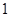 ,公比为
,公比为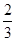 的等比数列
的等比数列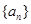 的前
的前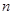 项和为
项和为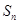 ,则( )
,则( )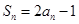

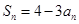
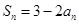
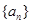 的公比
的公比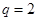 ,则
,则 .
. 项和是前
项和是前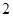 项和的
项和的 倍,则此数列的公比为( )
倍,则此数列的公比为( )

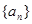 的公比为
的公比为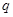 ,其前
,其前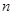 项的积为
项的积为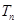 ,并且满足条件
,并且满足条件
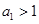 ,
,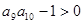 ,
,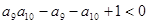 。给出下列结论:①
。给出下列结论:①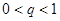 ;②
;②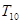 的值是
的值是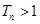 成立的最大自然数
成立的最大自然数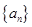 的前n项和为
的前n项和为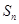 ,
,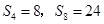 ,则
,则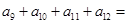 __________
__________ 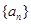 中,
中,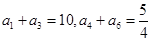 ,则公比
,则公比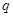 等于( )
等于( )