题目内容
已知函数f(x)=eax-x ,其中a≠0.若对一切x∈R,f(x)≥0恒成立,则a的取值集合 .
,其中a≠0.若对一切x∈R,f(x)≥0恒成立,则a的取值集合 .

解析试题分析:若 ,则对一切
,则对一切 ,
, ,这与题设矛盾.又
,这与题设矛盾.又 ,故
,故 .
.
而 ,令
,令 得
得 .
.
当 时,
时, ,
, 单调递减;当
单调递减;当 时,
时, ,
, 单调递增.故当x
单调递增.故当x ,
, 取最小值
取最小值 .
.
于是对一切 ,
, 恒成立,当且仅当
恒成立,当且仅当 . ①
. ①
令 ,则
,则 .
.
当 时,
时, ,
, 单调递增;当
单调递增;当 时,
时, ,
, 单调递减.
单调递减.
故当 时,
时, 取最大值
取最大值 .
.
因此,当且仅当 ,即
,即 时,①式成立.综上所述,
时,①式成立.综上所述, 的取值集合为
的取值集合为 .
.
考点:用导数研究函数的单调性及最值问题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 以速度
以速度 (
( 的单位:
的单位: ,
, 的单位:
的单位: )在一直线上运动,在此直线上
)在一直线上运动,在此直线上  在物体
在物体 处以
处以 (
( .
. 为一次函数,且
为一次函数,且 ,则
,则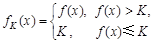 (K为给定常数),已知函数
(K为给定常数),已知函数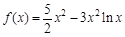 ,若对于任意的
,若对于任意的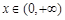 ,恒有
,恒有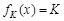 ,则实数K的取值范围为
,则实数K的取值范围为 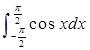 的值为2;②若
的值为2;②若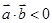 ,则
,则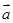 与
与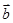 的夹角为钝角;③若
的夹角为钝角;③若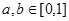 ,则不等式
,则不等式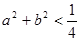 成立的概率是
成立的概率是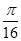 ;④函数
;④函数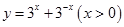 的最小值为2.
的最小值为2. .
. 在点
在点 处的切线方程为
处的切线方程为 ,则曲线
,则曲线 在点
在点 处切线的方程为 .
处切线的方程为 .
 (0≤x≤2π)的图象围成的封闭图形的面积为________.
(0≤x≤2π)的图象围成的封闭图形的面积为________.