题目内容
(1)讨论函数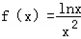 (x∈[e﹣1,e])的图象与直线y=k的交点个数.
(x∈[e﹣1,e])的图象与直线y=k的交点个数.
(2)求证:对任意的n∈N*,不等式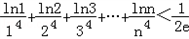 总成立.
总成立.
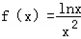 (x∈[e﹣1,e])的图象与直线y=k的交点个数.
(x∈[e﹣1,e])的图象与直线y=k的交点个数.(2)求证:对任意的n∈N*,不等式
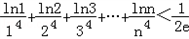 总成立.
总成立.(1)解:由题意得: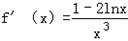 .
.
令f'(x)=0,得x=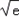 .
.
当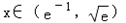 时,f'(x)>0,故函数f(x)在
时,f'(x)>0,故函数f(x)在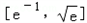 上递增;
上递增;
当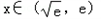 时,f'(x)<0,故函数f(x)在
时,f'(x)<0,故函数f(x)在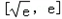 上递减.
上递减.
又因为f(e﹣1)=﹣e2,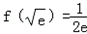 ,
,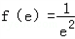 ,
,
所以当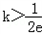 或k<﹣e2时,没有交点;
或k<﹣e2时,没有交点;
当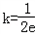 或
或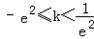 时,有唯一的交点;
时,有唯一的交点;
当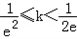 时,有两个交点.
时,有两个交点.
(2)证明:由(1)知函数f(x)在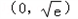 上递增,在
上递增,在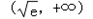 上递减,
上递减,
故f(x)在(0,+∞)上的最大值为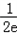 .即对x∈(0,+∞)均有
.即对x∈(0,+∞)均有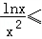
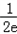 ,
,
故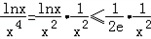 .
.
当n=1时,结论显然成立;
当n≥2时,有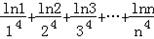 =
=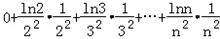 ≤
≤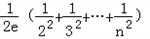 <
<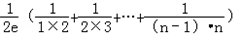 =
=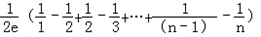 =
=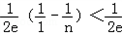 .
.
综上可知,对任意的n∈N*,不等式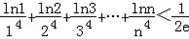 成立.
成立.
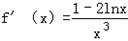 .
.令f'(x)=0,得x=
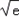 .
.当
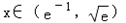 时,f'(x)>0,故函数f(x)在
时,f'(x)>0,故函数f(x)在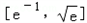 上递增;
上递增;当
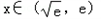 时,f'(x)<0,故函数f(x)在
时,f'(x)<0,故函数f(x)在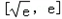 上递减.
上递减.又因为f(e﹣1)=﹣e2,
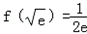 ,
,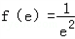 ,
,所以当
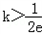 或k<﹣e2时,没有交点;
或k<﹣e2时,没有交点;当
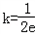 或
或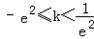 时,有唯一的交点;
时,有唯一的交点;当
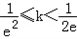 时,有两个交点.
时,有两个交点.(2)证明:由(1)知函数f(x)在
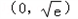 上递增,在
上递增,在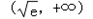 上递减,
上递减,故f(x)在(0,+∞)上的最大值为
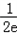 .即对x∈(0,+∞)均有
.即对x∈(0,+∞)均有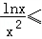
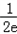 ,
,故
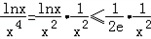 .
.当n=1时,结论显然成立;
当n≥2时,有
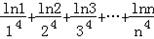 =
=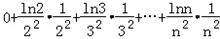 ≤
≤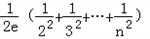 <
<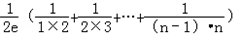 =
=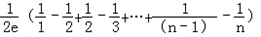 =
=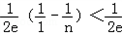 .
.综上可知,对任意的n∈N*,不等式
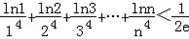 成立.
成立.
练习册系列答案
相关题目
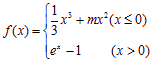 (1)讨论函数f (x)的极值情况; (2)设g (x) = ln(x + 1),当x1>x2>0时,试比较f (x1 – x2)与g (x1 – x2)及g (x1) –g (x2)三者的大小;并说明理由.
(1)讨论函数f (x)的极值情况; (2)设g (x) = ln(x + 1),当x1>x2>0时,试比较f (x1 – x2)与g (x1 – x2)及g (x1) –g (x2)三者的大小;并说明理由.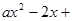 1 .
1 .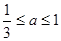 ,且f(x)在区间[1,3]上的最大值为M(a) ,最小值为N(a),
,且f(x)在区间[1,3]上的最大值为M(a) ,最小值为N(a),