题目内容
(1)讨论函数f(x)=
(x∈[e-1,e])的图象与直线y=k的交点个数.
(2)求证:对任意的n∈N*,不等式
+
+
+…+
<
总成立.
| lnx |
| x2 |
(2)求证:对任意的n∈N*,不等式
| ln1 |
| 14 |
| ln2 |
| 24 |
| ln3 |
| 34 |
| lnn |
| n4 |
| 1 |
| 2e |
分析:(1)利用导数判断f(x)在[e-1,
]上递增,函数f(x)在[
,e]上递减,由此求得函数的值域,从而得到f(x)图象与直线y=k的交点个数.
(2)根据函数的单调性求得f(x)在(0,+∞)上的最大值为
,x∈(0,+∞)时,
=
•
≤
•
,
用数学归纳法,结合放缩法证明不等式成立.
| e |
| e |
(2)根据函数的单调性求得f(x)在(0,+∞)上的最大值为
| 1 |
| 2e |
| lnx |
| x4 |
| lnx |
| x2 |
| 1 |
| x2 |
| 1 |
| 2e |
| 1 |
| x2 |
用数学归纳法,结合放缩法证明不等式成立.
解答:(1)解:由题意得:f′(x)=
.令f'(x)=0,得x=
.
当x∈(e-1,
)时,f'(x)>0,故函数f(x)在[e-1,
]上递增;
当x∈(
,e)时,f'(x)<0,故函数f(x)在[
,e]上递减.
又因为f(e-1)=-e2,f(
)=
,f(e)=
,所以当k>
或k<-e2时,没有交点;
当k=
或-e2≤k<
时,有唯一的交点;当
≤k<
时,有两个交点.
(2)证明:由(1)知函数f(x)在(0,
)上递增,在(
,+∞)上递减,
故f(x)在(0,+∞)上的最大值为
.
即对x∈(0,+∞)均有
≤
,故
=
•
≤
•
.
当n=1时,结论显然成立;当n≥2时,有
+
+
+…+
=0+
•
+
•
+…+
•
≤
(
+
+…+
)
<
(
+
+…+
)=
(
-
+
-
+…+
-
)
=
(
-
)<
.
综上可知,对任意的n∈N*,不等式
+
+
+…+
<
成立.
| 1-2lnx |
| x3 |
| e |
当x∈(e-1,
| e |
| e |
当x∈(
| e |
| e |
又因为f(e-1)=-e2,f(
| e |
| 1 |
| 2e |
| 1 |
| e2 |
| 1 |
| 2e |
当k=
| 1 |
| 2e |
| 1 |
| e2 |
| 1 |
| e2 |
| 1 |
| 2e |
(2)证明:由(1)知函数f(x)在(0,
| e |
| e |
故f(x)在(0,+∞)上的最大值为
| 1 |
| 2e |
即对x∈(0,+∞)均有
| lnx |
| x2 |
| 1 |
| 2e |
| lnx |
| x4 |
| lnx |
| x2 |
| 1 |
| x2 |
| 1 |
| 2e |
| 1 |
| x2 |
当n=1时,结论显然成立;当n≥2时,有
| ln1 |
| 14 |
| ln2 |
| 24 |
| ln3 |
| 34 |
| lnn |
| n4 |
=0+
| ln2 |
| 22 |
| 1 |
| 22 |
| ln3 |
| 32 |
| 1 |
| 32 |
| lnn |
| n2 |
| 1 |
| n2 |
| 1 |
| 2e |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
<
| 1 |
| 2e |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| (n-1)•n |
| 1 |
| 2e |
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| (n-1) |
| 1 |
| n |
=
| 1 |
| 2e |
| 1 |
| 1 |
| 1 |
| n |
| 1 |
| 2e |
综上可知,对任意的n∈N*,不等式
| ln1 |
| 14 |
| ln2 |
| 24 |
| ln3 |
| 34 |
| lnn |
| n4 |
| 1 |
| 2e |
点评:本题主要考查用放缩法证明不等式,利用导数研究函数的单调性,求函数的值域,用数学归纳法证明不等式,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
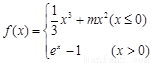
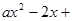 1 .
1 .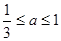 ,且f(x)在区间[1,3]上的最大值为M(a) ,最小值为N(a),
,且f(x)在区间[1,3]上的最大值为M(a) ,最小值为N(a),