Question

（2013•铁岭模拟）已知四边形ABCD满足AD∥BC，BA=AD=DC=

1

2

BC=a，E是BC的中点，将△BAE沿着AE翻折成△B₁AE，使面B₁AE⊥面AECD，F为B₁D的中点．
（Ⅰ）求四棱B₁-AECD的体积；
（Ⅱ）证明：B₁E∥面ACF；
（Ⅲ）求面ADB₁与面ECB₁所成二面角的余弦值．

Answer 1

分析：（Ⅰ）取AE的中点M，连接B₁M，证明B₁M⊥面AECD，从而可求四棱B₁-AECD的体积；
（Ⅱ）证明B₁E∥面ACF，利用线面平行的判定定理，证明FO∥B₁E即可；
（Ⅲ）连接MD，分别以ME，MD，MB₁为x，y，z轴建立空间直角坐标系，用坐标表示点与向量，求出面ECB₁与面ADB₁的法向量，利用向量的夹角公式，即可求得二面角的余弦值．

解答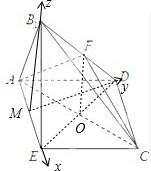：（Ⅰ）解：取AE的中点M，连接B₁M，因为BA=AD=DC=

1

2

BC=a，E是BC的中点，
所以△ABE为等边三角形，所以B1M=

3

2

a，
又因为面B₁AE⊥面AECD，所以B₁M⊥面AECD，…（2分）
所以V=

1

3

×

3

2

a×a×a×sin

π

3

=

a3

4

…（4分）
（Ⅱ）证明：连接ED交AC于O，连接OF，因为AECD为菱形，OE=OD，
又F为B₁D的中点，所以FO∥B₁E，
因为FO?面ACF
所以B₁E∥面ACF…（7分）
（Ⅲ）解：连接MD，分别以ME，MD，MB₁为x，y，z轴，建立空间直角坐标系．
则E(

a

2

，0，0)，C(a，

3

2

a，0)，A(-

a

2

，0，0)，D(0，

3

2

a，0)，B1(0，0，

3

2

a)

EC

=(

a

2

，

3 a

2

，0)，

EB1

=(-

a

2

，0，

3 a

2

)，

AD

=(

a

2

，

3 a

2

，0)，

AB1

=(

a

2

，0，

3 a

2

)…（9分）
设面ECB₁的法向量

v

=(x′，y′，z′)，则

a 2 x′+ 3 2 ay′=0 - a 2 x′+ 3 2 az′=0

，
令x'=1，则

u

=(1，-

3

3

，

3

3

)
设面ADB₁的法向量为

u

=(x，y，z)，则

a 2 x+ 3 2 ay=0 a 2 x+ 3 2 az=0

，
令x=1，则

v

=(1，-

3

3

，-

3

3

)…（11分）
则cos＜

u

，

v

＞=

1+ 1 3 - 1 3

1+ 1 3 + 1 3 × 1+ 1 3 + 1 3

=

3

5

，
所以二面角的余弦值为

3

5

…（12分）

点评：本题考查三棱锥的体积，考查线面平行，考查面面角，解题的关键是掌握线面平行的判定方法，利用空间向量解决面面角问题．