题目内容
给出命题:(1)某彩票的中奖概率为
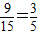 .,意味着买
.,意味着买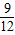 张彩票一定能中奖;
张彩票一定能中奖;(2)对立事件一定是互斥事件;
(3)若事件A、B满足P(A)+P(B)=1,则A、B为对立事件;
(4)从装有2个红球和2个白球的口袋中任取2个球,记事件A为“恰有1个白球”,记事件B=为“恰有2个白球”,则A,B为互斥而不对立的两个事件.
其中正确命题的个数是( )
A.3
B.2
C.1
D.0
【答案】分析:利用概率的概念可判断(1);由对立事件与互斥事件的概念可判断(2)、(4);由对立事件的概念可判断(3).
解答:解:(1)某彩票的中奖概率为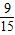 =
= ,说明买15张彩票,中奖的可能性约为
,说明买15张彩票,中奖的可能性约为 ,不是一定为
,不是一定为 ,故(1)错误;
,故(1)错误;
(2)有对立事件的概念可知,对立事件一定是互斥事件,故(2)正确;
(3)由对立事件的概念可知,若A、B为对立事件,则P(A)+P(B)=1,反之不然,故(3)错误;
(4)“恰有1个白球”发生时,“恰有2个白球”不会发生,即事件A与事件B为互斥事件,且在一次实验中不可能必有一个发生,故这两个事件并不对立;故(4)正确.
综上所述,正确命题的个数是(2)(4).
故选B.
点评:考查命题的真假判断与应用,考查对立事件与互斥事件的概念与概率公式,理解相关概念是解决问题的关键,属于中档题.
解答:解:(1)某彩票的中奖概率为
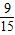 =
= ,说明买15张彩票,中奖的可能性约为
,说明买15张彩票,中奖的可能性约为 ,不是一定为
,不是一定为 ,故(1)错误;
,故(1)错误;(2)有对立事件的概念可知,对立事件一定是互斥事件,故(2)正确;
(3)由对立事件的概念可知,若A、B为对立事件,则P(A)+P(B)=1,反之不然,故(3)错误;
(4)“恰有1个白球”发生时,“恰有2个白球”不会发生,即事件A与事件B为互斥事件,且在一次实验中不可能必有一个发生,故这两个事件并不对立;故(4)正确.
综上所述,正确命题的个数是(2)(4).
故选B.
点评:考查命题的真假判断与应用,考查对立事件与互斥事件的概念与概率公式,理解相关概念是解决问题的关键,属于中档题.

练习册系列答案
相关题目