题目内容
(本题满分12分)
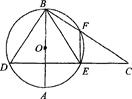
如图所示,已知PA切圆O于A,割线PBC交圆O于B、C,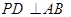 于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF。
于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF。
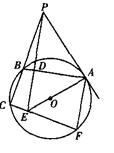
(1)求证:B,C,E,D四点共圆;
(2)当AB=12,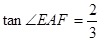 时,求圆O的半径.
时,求圆O的半径.
如图所示,已知PA切圆O于A,割线PBC交圆O于B、C,
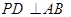 于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF。
于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF。
(1)求证:B,C,E,D四点共圆;
(2)当AB=12,
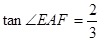 时,求圆O的半径.
时,求圆O的半径.(1)见解析;(2)圆O的半径 。
。
 。
。本试题主要是考查了几何证明的运用。圆内的性质和三角形的相似的运用。
(1)由切割线定理
由已知易得 ∽
∽ ,所以
,所以
(2)由(1)知
再结合平行的性质的得到 ,然后结合勾股定理得到结论。
,然后结合勾股定理得到结论。
解:(1)由切割线定理
由已知易得 ∽
∽ ,所以
,所以
所以 =
= 又
又 为公共角,所以
为公共角,所以 ∽
∽ ,…………3分
,…………3分
所以,
所以,B,C,E,D四点共圆 ……………………………………….4分
(2)作 于
于 ,
,

由(1)知
 ,
,



在 中,
中,

所以,圆O的半径 。 ……………………………….12分
。 ……………………………….12分
(1)由切割线定理

由已知易得
 ∽
∽ ,所以
,所以
(2)由(1)知

再结合平行的性质的得到
 ,然后结合勾股定理得到结论。
,然后结合勾股定理得到结论。解:(1)由切割线定理

由已知易得
 ∽
∽ ,所以
,所以
所以
 =
= 又
又 为公共角,所以
为公共角,所以 ∽
∽ ,…………3分
,…………3分所以,

所以,B,C,E,D四点共圆 ……………………………………….4分
(2)作
 于
于 ,
,
由(1)知

 ,
,



在
 中,
中,

所以,圆O的半径
 。 ……………………………….12分
。 ……………………………….12分
练习册系列答案
相关题目
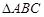 内接于⊙
内接于⊙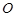 ,
, 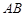 是⊙
是⊙ 是过点
是过点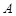 的直线, 且
的直线, 且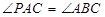 .
.
 交
交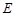 ,
,  ,
,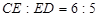 ,
,  , 求
, 求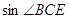 .
.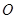 的半径OB垂直于直径AC,
的半径OB垂直于直径AC,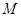 为AO上一点,
为AO上一点, 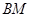 的延长线交⊙
的延长线交⊙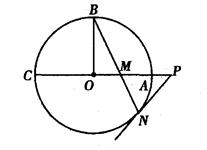
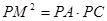 ;
;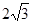 ,OA=
,OA=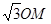 ,求
,求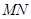 的长.
的长.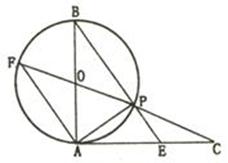

 所示,过圆
所示,过圆 外一点
外一点 做一条直线与圆
做一条直线与圆 两点,
两点, ,
, 与圆
与圆 点.已知圆
点.已知圆 ,
, ,则
,则 ______ .
______ . 
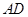 是
是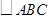 的高,
的高,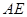 是
是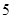 ,
,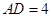 ,
,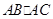 的值。
的值。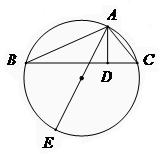
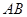 是⊙
是⊙ 的直径,
的直径,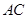 是⊙
是⊙ 的平分线
的平分线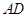 交⊙
交⊙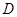 ,过点
,过点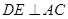 交
交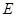 ,
,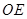 交
交 .若
.若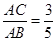 ,则
,则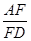 的值为 .
的值为 .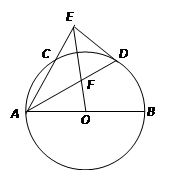
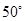 ,求∠IEH的度数.
,求∠IEH的度数.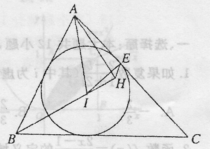
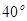 ,则∠DEB___________
,则∠DEB___________